/Szkoła średnia/Równania/Wielomianowe/Stopnia 3

Zadanie nr 9662230

Dodaj do ulubionych
Dodaj do rozwiązanych

Sprawdź dla jakiego 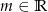m ∈ R pierwiastki wielomianu 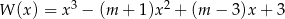3 2 W (x ) = x − (m + 1)x + (m − 3)x + 3 tworzą ciąg arytmetyczny?

Rozwiązanie

Sposób I

Spróbujmy przez chwilę nie przejmować się podanym warunkiem i normalnie sprawdźmy, czy podane równanie nie ma przypadkiem pierwiastka wymiernego. Sprawdzając dzielniki wyrazu wolnego znajdujemy pierwiastek 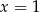x = 1 . Dzielimy więc podany wielomian przez 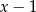x − 1 . My zrobimy to grupując wyrazy.

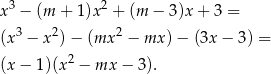
x3 − (m + 1)x2 + (m − 3)x+ 3 = (x3 − x2) − (mx 2 − mx ) − (3x − 3) = 2 (x − 1)(x − mx − 3).

Zauważmy jeszcze, że równanie kwadratowe w drugim nawiasie ma zawsze dwa rozwiązania, bo

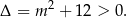
Δ = m 2 + 12 > 0.

Na mocy wzorów Viète’a pierwiastki 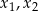x1,x 2 tego równania spełniają warunki

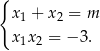
{ x1 + x2 = m x1x2 = − 3.

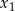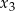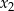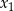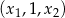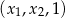Z drugiego warunku wynika, że liczby x1 i x3 różnią się znakiem, co oznacza, że wyjściowy wielomian ma dwa pierwiastki dodatnie (powiedzmy 1 i x 2 ) i jeden ujemny x1 . Wiemy, że liczby te tworzą ciąg arytmetyczny, ale nie wiemy w jakiej dokładnie kolejności – są możliwe dwie sytuacje: (x1,1,x 2) i (x1,x 2,1) .

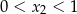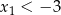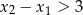Zauważmy, że druga sytuacja prowadzi do sprzeczności, bo wtedy 0 < x2 < 1 , co na mocy wzorów Viète’a oznacza, że x1 < − 3 . To jednak nie jest możliwe, bo wtedy x2 − x1 > 3 , a 1− x2 < 1 .

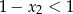Arytmetyczny jest więc ciąg 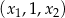(x1,1,x2) , co możemy zapisać w postaci

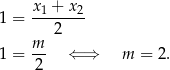
x + x 1 = -1----2- 2 1 = m- ⇐ ⇒ m = 2. 2

Możemy sprawdzić (choć nie musimy), że dla 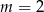m = 2 dany wielomian ma pierwiastki: − 1,1,3 .

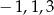Sposób II

Okazuje się, że podobnie jak dla równania kwadratowego, istnieją wzory Viète’a dla równań wyższych stopni. Dla równania stopnia 3 mają one postać

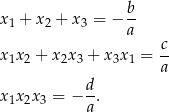
b- x1 + x2 + x3 = − a c- x1x 2 + x 2x3 + x3x1 = a d x1x 2x3 = − --. a

gdzie 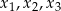x1,x2,x 3 są pierwiastkami równania 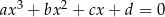3 2 ax + bx + cx+ d = 0 . Wzory te łatwo uzasadnić porównując współczynniki po obu stronach równości

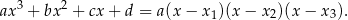
3 2 ax + bx + cx + d = a(x− x1)(x − x2)(x − x3).

Załóżmy, że pierwiastki 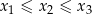x1 ≤ x2 ≤ x 3 danego wielomianu tworzą ciąg arytmetyczny, tzn. 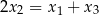2x 2 = x1 + x3 Na mocy powyższych wzorów mamy

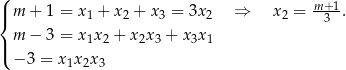
( |{ m + 1 = x1 + x2 + x3 = 3x 2 ⇒ x2 = m-+1. 3 | m − 3 = x1x2 + x2x3 + x3x 1 ( − 3 = x1x2x 3

Mnożymy teraz drugie równanie przez 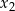x 2 i korzystamy z dwóch pozostałych równań.

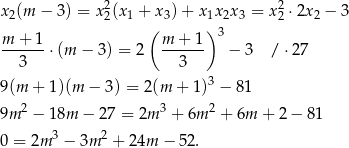
x (m − 3) = x2(x + x ) + x x x = x2 ⋅2x − 3 2 2 1 ( 3 1) 2 3 2 2 m + 1 m + 1 3 --3--- ⋅(m − 3 ) = 2 --3--- − 3 / ⋅27 9(m + 1)(m − 3 ) = 2(m + 1 )3 − 81 2 3 2 9m − 18m − 27 = 2m + 6m + 6m + 2 − 81 0 = 2m 3 − 3m 2 + 24m − 52.

Szukamy teraz pierwiastków wymiernych tego wielomianu – można sprawdzić, że jednym z nich jest 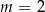m = 2 . Dzielimy zatem ten wielomian przez 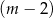(m − 2) . Zrobimy to grupując wyrazy.

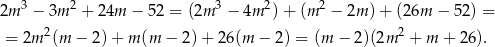
2m 3 − 3m 2 + 24m − 52 = (2m 3 − 4m 2) + (m 2 − 2m )+ (2 6m − 52 ) = 2 2 = 2m (m − 2)+ m (m − 2)+ 26(m − 2) = (m − 2)(2m + m + 26).

Łatwo sprawdzić, że trójmian w drugim nawiasie nie ma pierwiastków, więc jedynym rozwiązaniem jest 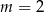m = 2 . Mamy wtedy 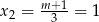x = m+1-= 1 2 3 i wyjściowy wielomian przyjmuje postać

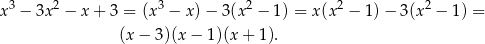
x 3 − 3x 2 − x+ 3 = (x3 − x) − 3(x2 − 1) = x (x2 − 1)− 3(x2 − 1) = (x − 3)(x − 1)(x + 1).

Pierwiastkiem tego wielomianu są więc liczby 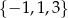{− 1,1,3} , które oczywiście tworzą ciąg arytmetyczny.  
Odpowiedź: m = 2

Wersja PDF