/Szkoła średnia/Zadania maturalne/Matura 2021/Matura próbna
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis zadania.info poziom podstawowy 6 marca 2021 Czas pracy: 170 minut
Zadania zamknięte
Wartość wyrażenia 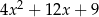 dla
dla 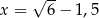 jest równa
jest równa
A) 12 B) 24 C) 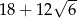 D)
D) 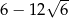
Liczba 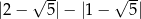 jest równa
jest równa
A) 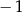 B)
B) 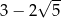 C) 1 D)
C) 1 D) 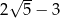
Liczba 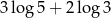 jest równa
jest równa
A) 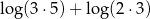 B)
B) 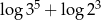
C) 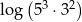 D)
D) 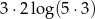
Przed podwyżką cena pączka i drożdżówki była taka sama. Cenę pączka podniesiono o 20%, a za drożdżówkę trzeba zapłacić o 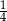 więcej. Zatem za cztery drożdżówki i sześć pączków trzeba teraz zapłacić więcej o
więcej. Zatem za cztery drożdżówki i sześć pączków trzeba teraz zapłacić więcej o
A) 20% B) 22% C) 25% D) 23%
Zbiorem wszystkich rozwiązań nierówności 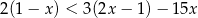 jest przedział
jest przedział
A) 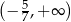 B)
B) 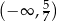 C)
C) 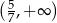 D)
D) 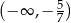
Po usunięciu niewymierności z mianownika ułamka 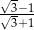 otrzymamy liczbę:
otrzymamy liczbę:
A) 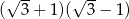 B)
B) 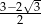 C)
C) 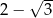 D)
D) 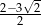
Do zbioru rozwiązań nierówności 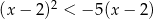 należy liczba
należy liczba
A) 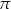 B)
B) 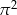 C)
C) 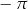 D)
D) 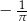
Odległość między prostymi 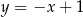 i
i 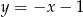 jest równa
jest równa
A) 2 B) 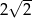 C) 1 D)
C) 1 D) 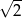
Prosta 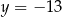 przecina wykres funkcji kwadratowej
przecina wykres funkcji kwadratowej 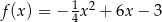 w punktach
w punktach 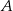 i
i 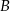 . Środek odcinka
. Środek odcinka 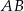 leży na prostej o równaniu
leży na prostej o równaniu
A) 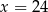 B)
B) 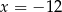 C)
C) 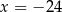 D)
D) 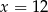
Ciąg 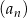 jest określony wzorem
jest określony wzorem 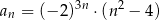 dla
dla 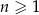 . Wówczas
. Wówczas
A) 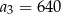 B)
B) 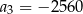 C)
C) 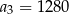 D)
D) 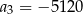
Na rysunku przedstawiono fragment wykresu funkcji liniowej 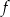 określonej wzorem
określonej wzorem 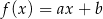 .
.
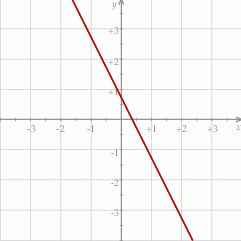
Współczynniki  oraz
oraz 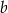 we wzorze funkcji
we wzorze funkcji 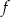 spełniają zależność
spełniają zależność
A) 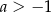 i
i 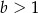 B)
B) 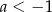 i
i 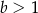 C)
C) 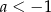 i
i 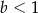 D)
D) 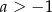 i
i 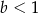
Rozwiązaniem równania 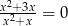 jest liczba
jest liczba
A) 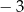 B) 0 C) 3 D) 9
B) 0 C) 3 D) 9
Prosta o równaniu 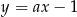 jest prostopadła do prostej o równaniu
jest prostopadła do prostej o równaniu 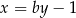 . Stąd wynika, że
. Stąd wynika, że
A) 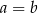 B)
B) 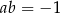 C)
C) 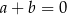 D)
D) 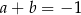
Kąt  jest ostry i
jest ostry i 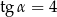 . Wobec tego
. Wobec tego
A) 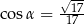 B)
B) 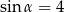 i
i 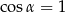 C)
C) 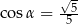 D)
D) 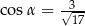
W ciągu arytmetycznym 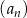 , określonym dla
, określonym dla 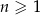 , czwarty wyraz jest równy 5, a różnica tego ciągu jest równa 3. Suma
, czwarty wyraz jest równy 5, a różnica tego ciągu jest równa 3. Suma 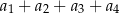 jest równa
jest równa
A) 2 B) 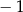 C) 12 D) 5
C) 12 D) 5
Przekątne trapezu 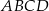 przecinają się w punkcie
przecinają się w punkcie 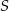 w ten sposób, że pole trójkąta
w ten sposób, że pole trójkąta 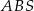 jest 4 razy większe od pola trójkąta
jest 4 razy większe od pola trójkąta 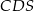 .
.
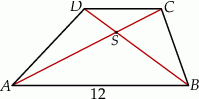
Jeżeli podstawa 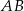 ma długość 12, to długość podstawy
ma długość 12, to długość podstawy 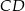 jest równa
jest równa
A) 8 B) 3 C) 6 D) 9
Zbiorem wartości funkcji kwadratowej 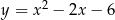 jest przedział
jest przedział
A) 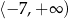 B)
B) 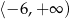 C)
C) 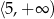 D)
D) 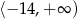
Funkcja 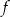 jest określona wzorem
jest określona wzorem 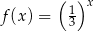 dla wszystkich liczb rzeczywistych
dla wszystkich liczb rzeczywistych  . Funkcja
. Funkcja 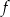 dla argumentu
dla argumentu 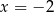 przyjmuje wartość
przyjmuje wartość
A)  B)
B) 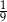 C) 6 D) 9
C) 6 D) 9
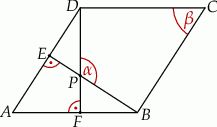
Wysokości 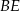 i
i 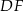 rombu
rombu 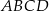 przecinają się w punkcie
przecinają się w punkcie  (zobacz rysunek).
(zobacz rysunek).
Wyrażenie 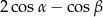 jest równe
jest równe
A) 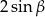 B)
B) 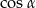 C) 0 D)
C) 0 D) 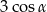
Punkty 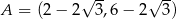 ,
, 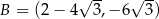 ,
, 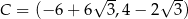 są kolejnymi wierzchołkami równoległoboku
są kolejnymi wierzchołkami równoległoboku 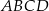 . Przekątne tego równoległoboku przecinają się w punkcie
. Przekątne tego równoległoboku przecinają się w punkcie
A) 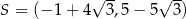 B)
B) 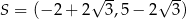
C) 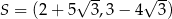 D)
D) 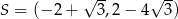
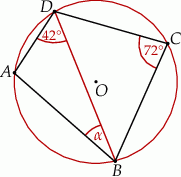
Punkty  leżą na okręgu o środku
leżą na okręgu o środku  (zobacz rysunek). Miara zaznaczonego kąta
(zobacz rysunek). Miara zaznaczonego kąta  jest równa
jest równa
A) 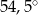 B)
B) 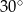 C)
C) 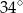 D)
D) 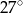
Pole równoległoboku o bokach długości 4 i 7 oraz kącie rozwartym 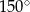 jest równe
jest równe
A) 14 B) 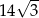 C)
C) 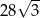 D) 28
D) 28
Cztery liczby: 2, 3,  , 8, tworzące zestaw danych, są uporządkowane rosnąco. Mediana tego zestawu czterech danych jest równa medianie zestawu pięciu danych: 7, 2, 4, 9, 1. Zatem
, 8, tworzące zestaw danych, są uporządkowane rosnąco. Mediana tego zestawu czterech danych jest równa medianie zestawu pięciu danych: 7, 2, 4, 9, 1. Zatem
A) 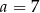 B)
B) 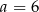 C)
C) 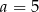 D)
D) 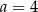
Ile jest wszystkich liczb naturalnych dodatnich mniejszych od 2021, których cyfra jedności jest jedną z cyfr: 0, 2, 6, 8?
A) 1010 B) 808 C) 606 D) 560
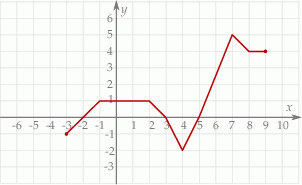
Korzystając z danego wykresu funkcji 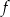 , wskaż nierówność prawdziwą
, wskaż nierówność prawdziwą
A) 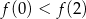 B)
B) 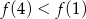 C)
C) 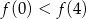 D)
D) 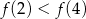
Ze zbioru dzielników naturalnych liczby 12 losujemy dwa razy po jednej liczbie (otrzymane liczby mogą się powtarzać). Prawdopodobieństwo, że iloczyn wybranych liczb jest dzielnikiem liczby 6 jest równe
A) 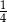 B)
B) 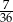 C)
C)  D)
D) 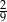
Każda krawędź ostrosłupa prawidłowego trójkątnego ma długość 12 (ostrosłup taki jest nazywany czworościanem foremnym). Wysokość tego ostrosłupa jest równa
A) 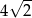 B)
B) 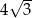 C)
C) 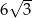 D)
D) 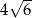
Walec ma objętość 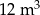 . Stożek o takiej samej wysokości i takim samym promieniu podstawy ma objętość równą:
. Stożek o takiej samej wysokości i takim samym promieniu podstawy ma objętość równą:
A) 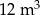 B)
B) 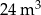 C)
C) 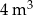 D)
D) 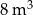
Zadania otwarte
Rozwiąż równanie 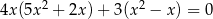 .
.
Kąt  jest ostry i spełnia warunek
jest ostry i spełnia warunek 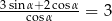 . Oblicz tangens kąta
. Oblicz tangens kąta  .
.
Wyznacz współrzędne punktu przecięcia przekątnych czworokąta 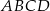 jeżeli
jeżeli 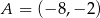 ,
, 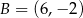 ,
, 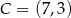 i
i 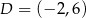 .
.
Wykaż, że dla dowolnych liczb rzeczywistych  i
i 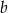 prawdziwa jest nierówność
prawdziwa jest nierówność
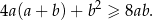
Oblicz sumę dziewięciu początkowych wyrazów rosnącego ciągu geometrycznego 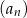 , określonego dla
, określonego dla 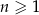 , w którym
, w którym 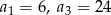 .
.
W pudełku są 24 kule, z czego 15 białych i 9 czarnych. Do tego pudełka dołożono pewną liczbę kul białych i trzy razy większą liczbę kul czarnych, a następnie wylosowano jedną kulę z pudełka. Prawdopodobieństwo, że wylosowana kula jest biała jest równe 0,34. Ile kul czarnych dołożono do pudełka?
Dany jest graniastosłup prawidłowy trójkątny 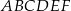 o podstawach
o podstawach 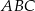 i
i 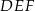 i krawędziach bocznych
i krawędziach bocznych 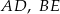 i
i 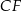 , które mają długość 13. Oblicz pole powierzchni całkowitej i objętość tego graniastosłupa jeżeli pole trójkąta
, które mają długość 13. Oblicz pole powierzchni całkowitej i objętość tego graniastosłupa jeżeli pole trójkąta 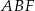 stanowi
stanowi 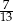 pola ściany bocznej
pola ściany bocznej 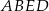 .
.

