/Szkoła średnia/Zadania maturalne/Matura 2021/Matura próbna
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis zadania.info poziom podstawowy 27 lutego 2021 Czas pracy: 170 minut
Zadania zamknięte
Wartość wyrażenia 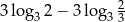 jest równa
jest równa
A) 4 B) 2 C) 3 D) 1
Liczba 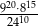 jest równa
jest równa
A) 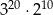 B)
B) 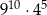 C)
C) 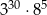 D)
D) 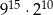
Wyrażenie 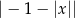 dla
dla 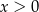 jest równe
jest równe
A) 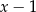 B)
B) 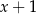 C)
C) 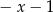 D)
D) 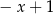
Wskaż największą liczbę całkowitą spełniającą nierówność 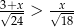 .
.
A) 9 B) 17 C) 13 D) 19
Jeżeli 8,5% liczby  jest równe 163,2, to liczba
jest równe 163,2, to liczba  jest równa
jest równa
A) 19200 B) 1920 C) 1387,2 D) 13872
Wskaż równanie, dla którego suma wszystkich rozwiązań jest równa 0.
A) 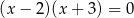 B)
B) 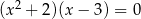
C) 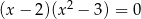 D)
D) 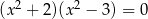
Dla każdych liczb rzeczywistych 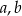 wyrażenie
wyrażenie 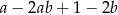 jest równe
jest równe
A) 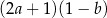 B)
B) 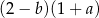 C)
C) 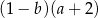 D)
D) 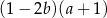
Zbiorem wartości funkcji kwadratowej 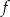 określonej wzorem
określonej wzorem 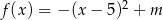 jest przedział
jest przedział 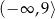 . Wtedy
. Wtedy
A) 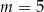 B)
B) 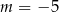 C)
C) 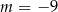 D)
D) 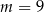
Liczbą większą od 3 jest
A) 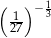 B)
B) 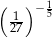 C)
C) 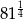 D)
D) 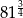
Liczba 991 jest liczbą pierwszą. Liczba dzielników naturalnych liczby 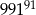 jest równa
jest równa
A) 182 B) 92 C) 91 D) 89
Dany jest trójkąt równoramienny, w którym ramię o długości 10 tworzy z podstawą kąt 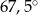 . Pole tego trójkąta jest równe
. Pole tego trójkąta jest równe
A) 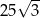 B)
B) 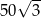 C)
C) 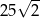 D)
D) 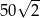
Funkcja 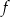 jest określona wzorem
jest określona wzorem 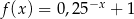 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Liczba
. Liczba 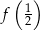 jest równa
jest równa
A) 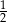 B)
B) 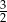 C) 3 D) 17
C) 3 D) 17
W trapez 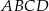 wpisano koło
wpisano koło 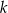 , które jest styczne do podstaw trapezu w punktach
, które jest styczne do podstaw trapezu w punktach 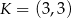 i
i 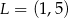 . Pole koła
. Pole koła 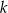 jest równe
jest równe
A) 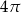 B)
B) 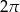 C)
C) 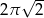 D)
D) 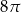
Prostą równoległą do prostej o równaniu 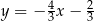 jest prosta opisana równaniem
jest prosta opisana równaniem
A) 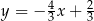 B)
B) 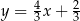 C)
C) 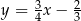 D)
D) 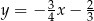
W ciągu arytmetycznym 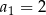 oraz
oraz 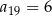 . Wtedy suma
. Wtedy suma 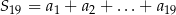 jest równa
jest równa
A) 76 B) 80 C) 152 D) 160
Punkt 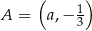 należy do wykresu funkcji liniowej
należy do wykresu funkcji liniowej 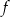 określonej wzorem
określonej wzorem 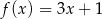 . Wynika stąd, że
. Wynika stąd, że
A) 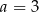 B)
B) 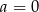 C)
C) 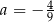 D)
D) 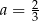
Kąt  jest ostry oraz
jest ostry oraz 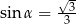 . Wtedy
. Wtedy
A) 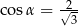 B)
B) 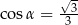 C)
C) 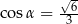 D)
D) 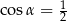
Układ równań 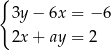 ma nieskończenie wiele rozwiązań, jeśli
ma nieskończenie wiele rozwiązań, jeśli
A) 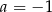 B)
B) 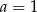 C)
C) 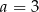 D)
D) 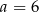
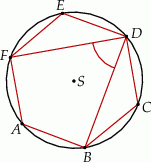
Punkty 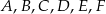 leżące na okręgu o środku
leżące na okręgu o środku  są wierzchołkami sześciokąta foremnego. Miara zaznaczonego na rysunku kąta wpisanego
są wierzchołkami sześciokąta foremnego. Miara zaznaczonego na rysunku kąta wpisanego 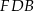 jest równa
jest równa
A) 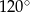 B)
B) 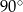 C)
C) 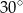 D)
D) 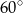
Punkt 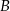 jest obrazem punktu
jest obrazem punktu 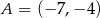 w symetrii względem początku układu współrzędnych. Długość odcinka
w symetrii względem początku układu współrzędnych. Długość odcinka 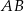 jest równa
jest równa
A) 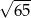 B)
B) 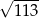 C)
C) 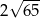 D) 13
D) 13
Wielkości  i
i 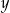 są odwrotnie proporcjonalne (tabela poniżej).
są odwrotnie proporcjonalne (tabela poniżej).
 |  | 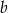 | 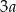 |  |
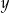 | 48 | 8 |  | 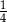 |
Stąd wynika, że
A) 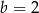 B)
B) 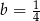 C)
C) 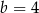 D)
D) 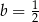
Na końcu naprężonej linki długości 18 m znajduje się latawiec. Linka tworzy z poziomem kąt 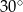 . Latawiec znajduje się nad ziemią na wysokości
. Latawiec znajduje się nad ziemią na wysokości
A) 6 m B) 12 m C) 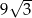 m D) 9 m
m D) 9 m
Wszystkich liczb czterocyfrowych parzystych, w których zapisie nie występują cyfry: 1, 2, 4, 8, 3, jest
A) 200 B) 625 C) 250 D) 500
Suma długości wszystkich krawędzi sześcianu jest o 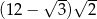 większa od długości przekątnej tego sześcianu. Pole powierzchni tego sześcianu jest równe
większa od długości przekątnej tego sześcianu. Pole powierzchni tego sześcianu jest równe
A) 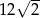 B) 12 C) 2 D)
B) 12 C) 2 D) 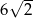
Dane są graniastosłup i ostrosłup o takich samych podstawach. Liczba wszystkich wierzchołków tego graniastosłupa jest o 10 większa od liczby wszystkich wierzchołków tego ostrosłupa. Podstawą każdej z tych brył jest
A) dziewięciokąt. B) ośmiokąt. C) jedenastokąt. D) dziesięciokąt.
Ze zbioru liczb naturalnych dwucyfrowych nie mniejszych od 40 losujemy jedną liczbę. Jakie jest prawdopodobieństwo, że wylosowana liczba będzie podzielna przez 5?
A) 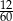 B)
B) 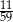 C)
C) 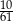 D)
D) 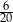
Promień kuli o polu powierzchni równym 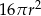 zmniejszono 2 razy. Objętość tak zmienionej kuli jest równa
zmniejszono 2 razy. Objętość tak zmienionej kuli jest równa
A) 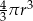 B)
B) 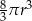 C)
C) 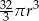 D)
D) 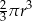
Średnia arytmetyczna zestawu danych: 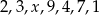 wynosi
wynosi 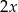 . Wynika z tego, że:
. Wynika z tego, że:
A) 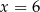 B)
B) 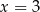 C)
C) 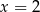 D)
D) 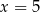
Zadania otwarte
Rozwiąż równanie 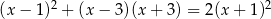 .
.
Z urny, w której jest 6 kul czarnych i 2 zielone, wyjęto dwa razy po jednej kuli ze zwracaniem. Oblicz prawdopodobieństwo, że wyjęto kule różnych kolorów.
Wykaż, że dla każdych dwóch liczb rzeczywistych  i
i 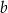 prawdziwa jest nierówność
prawdziwa jest nierówność
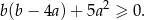
Dany jest trójkąt równoramienny 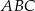 , w którym podstawa
, w którym podstawa 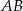 ma długość 32, a każde z ramion
ma długość 32, a każde z ramion 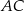 i
i 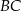 ma długość równą 34. Punkt
ma długość równą 34. Punkt 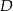 jest środkiem ramienia
jest środkiem ramienia 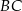 (zobacz rysunek).
(zobacz rysunek).
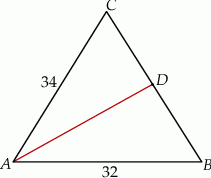
Oblicz długość odcinka 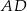 .
.
Dany jest czterowyrazowy ciąg 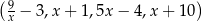 . Oblicz wszystkie wartości
. Oblicz wszystkie wartości  , dla których ten ciąg jest geometryczny.
, dla których ten ciąg jest geometryczny.
Bryła przedstawiona na poniższym rysunku powstała przez wycięcie z graniastosłupa prostego trójkątnego innego graniastosłupa prostego. Oblicz pole powierzchni tej bryły.
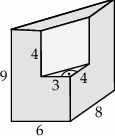
Dany jest trójkąt równoboczny 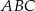 , w którym
, w którym 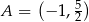 . Bok
. Bok 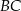 tego trójkąta jest zwarty w prostej o równaniu
tego trójkąta jest zwarty w prostej o równaniu 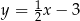 . Oblicz współrzędne środka odcinka
. Oblicz współrzędne środka odcinka 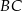 oraz oblicz pole trójkąta
oraz oblicz pole trójkąta 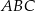 .
.

