/Szkoła średnia/Zadania maturalne/Matura 2021/Matura próbna
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis zadania.info poziom rozszerzony 13 marca 2021 Czas pracy: 180 minut
Zadania zamknięte
Suma
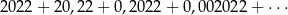
wszystkich wyrazów nieskończonego ciągu geometrycznego liczb rzeczywistych jest równa
A) 202200 B) 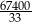 C) 67400 D)
C) 67400 D) 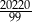
Granica ciągu 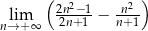 jest równa
jest równa
A) 1 B)  C)
C) 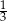 D)
D) 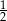
Liczba 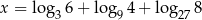 jest równa
jest równa
A) 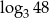 B)
B) 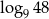 C)
C) 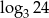 D)
D) 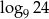
Niech 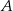 i
i 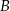 będą takim zdarzeniami losowymi, że
będą takim zdarzeniami losowymi, że 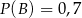 i
i 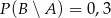 . Wtedy prawdopodobieństwo warunkowe
. Wtedy prawdopodobieństwo warunkowe 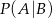 jest równe
jest równe
A) 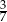 B)
B) 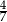 C)
C) 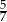 D)
D) 
Zadania otwarte
Oblicz granice jednostronne funkcji 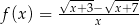 w punkcie
w punkcie 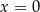 .
.
Wyznacz wszystkie wartości parametru  , dla których równanie
, dla których równanie 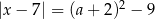 ma dwa różne rozwiązania dodatnie.
ma dwa różne rozwiązania dodatnie.
Na bokach trójkąta zbudowano kwadraty o polach 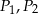 i
i 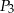 (zobacz rysunek)
(zobacz rysunek)
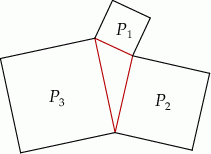
Wykaż, że 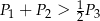 .
.
Wykres funkcji 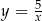 przesunięto o wektor
przesunięto o wektor ![→ v = [2,k]](https://img.zadania.info/zes/0093235/HzesT30x.gif) i otrzymano wykres funkcji
i otrzymano wykres funkcji 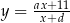 . Wyznacz
. Wyznacz 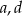 i
i 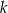 .
.
Wykaż, że
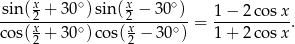
Funkcja 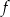 określona jest wzorem
określona jest wzorem 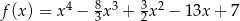 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Wyznacz równania tych stycznych do wykresu funkcji
. Wyznacz równania tych stycznych do wykresu funkcji 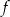 , które są równoległe do prostej o równaniu
, które są równoległe do prostej o równaniu 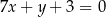 .
.
Oblicz miarę kąta między stycznymi do okręgu 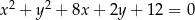 poprowadzonymi przez punkt
poprowadzonymi przez punkt 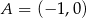 .
.
Trzy różne liczby całkowite tworzą ciąg geometryczny o ilorazie będącym ujemną liczbą całkowitą. Jeżeli najmniejszą z tych liczb zwiększymy o 16, to liczby te (w tej samej kolejności) są kolejnymi wyrazami ciągu arytmetycznego. Wyznacz te liczby.
Z pudełka, w którym jest 13 kul ponumerowanych kolejnymi liczbami od 1 do 13, losujemy bez zwracania 5 kul. Oblicz, jakie jest prawdopodobieństwo, że wśród wylosowanych kul jest dokładnie jedna para kul z sumą numerów równą 14.
Podstawą ostrosłupa 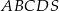 jest czworokąt wypukły
jest czworokąt wypukły 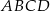 , w którym
, w którym 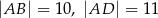 oraz
oraz 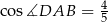 . Każda z krawędzi bocznych ostrosłupa ma długość 6. Oblicz wysokość ostrosłupa.
. Każda z krawędzi bocznych ostrosłupa ma długość 6. Oblicz wysokość ostrosłupa.
Wykres funkcji kwadratowej 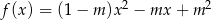 przecina oś
przecina oś 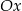 w punktach
w punktach 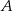 i
i 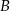 , które leżą po dwóch różnych stronach osi
, które leżą po dwóch różnych stronach osi 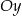 . Wyznacz tę wartość parametru
. Wyznacz tę wartość parametru 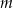 , dla której iloczyn odległości punktów
, dla której iloczyn odległości punktów 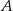 i
i 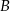 od początku układu współrzędnych jest najmniejszy możliwy. Dla wyznaczonej wartości
od początku układu współrzędnych jest najmniejszy możliwy. Dla wyznaczonej wartości 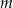 oblicz sumę odległości punktów
oblicz sumę odległości punktów 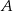 i
i 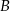 od początku układu współrzędnych.
od początku układu współrzędnych.

