/Szkoła średnia/Zadania maturalne/Matura 2021/Matura próbna/CKE, OKE, CEN
Próbny Egzamin Maturalny
z Matematyki (CKE)
poziom rozszerzony 10 marca 2021 Czas pracy: 180 minut
Zadania zamknięte
Liczba 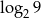 jest równa
jest równa
A) 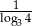 B)
B) 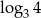 C)
C) 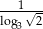 D)
D) 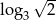
Dane są dwie urny z kulami. W pierwszej urnie jest 10 kul: 8 białych i 2 czarne, w drugiej jest 8 kul: 5 białych i 3 czarne. Wylosowanie każdej z urn jest jednakowo prawdopodobne. Wylosowano jedną z tych urn i wyciągnięto z niej losowo jedną kulę. Wyciągnięta kula była czarna. Prawdopodobieństwo zdarzenia, że wylosowana kula pochodziła z pierwszej z tych urn, jest równe
A) 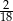 B)
B) 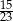 C)
C) 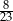 D)
D) 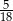
Prosta dana równaniem 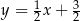 jest prostopadła do stycznej do wykresu funkcji
jest prostopadła do stycznej do wykresu funkcji
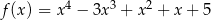
w punkcie
A) 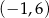 B)
B) 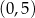 C)
C) 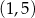 D)
D) 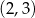
Liczba  jest sumą wszystkich wyrazów nieskończonego ciągu geometrycznego o pierwszym wyrazie równym 1 i ilorazie
jest sumą wszystkich wyrazów nieskończonego ciągu geometrycznego o pierwszym wyrazie równym 1 i ilorazie 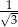 . Liczba
. Liczba 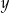 jest sumą wszystkich wyrazów nieskończonego ciągu geometrycznego o pierwszym wyrazie równym 1 i ilorazie
jest sumą wszystkich wyrazów nieskończonego ciągu geometrycznego o pierwszym wyrazie równym 1 i ilorazie 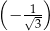 . Wynika stąd, że liczba
. Wynika stąd, że liczba 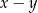 jest równa
jest równa
A) 0 B) 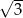 C)
C) 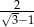 D) 3
D) 3
Zadania otwarte
Oblicz, ile jest liczb dziesięciocyfrowych takich, że suma cyfr w każdej z tych liczb jest równa 13 i żadna cyfra nie jest zerem.
Wykaż, że dla każdej liczby rzeczywistej  większej od 2 i dla każdej liczby rzeczywistej
większej od 2 i dla każdej liczby rzeczywistej 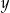 prawdziwa jest nierówność
prawdziwa jest nierówność 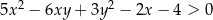 .
.
Rozwiąż równanie
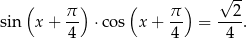
Na przeciwprostokątnej 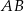 trójkąta prostokątnego
trójkąta prostokątnego 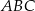 zbudowano kwadrat
zbudowano kwadrat 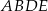 .
.
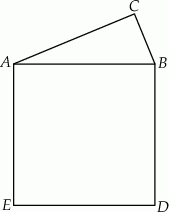
Stosunek pola trójkąta do pola kwadratu jest równy 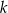 . Wykaż, że suma tangensów kątów ostrych tego trójkąta jest równa
. Wykaż, że suma tangensów kątów ostrych tego trójkąta jest równa 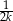 .
.
Czworokąt 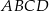 jest wpisany w okrąg o promieniu
jest wpisany w okrąg o promieniu 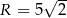 . Przekątna
. Przekątna 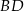 tego czworokąta ma długość 10. Kąty wewnętrzne
tego czworokąta ma długość 10. Kąty wewnętrzne 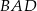 i
i 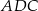 czworokąta
czworokąta 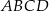 są ostre, a iloczyn sinusów wszystkich jego kątów wewnętrznych jest równy
są ostre, a iloczyn sinusów wszystkich jego kątów wewnętrznych jest równy  . Oblicz miary kątów wewnętrznych tego czworokąta.
. Oblicz miary kątów wewnętrznych tego czworokąta.
Reszty z dzielenia wielomianu 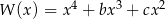 przez dwumiany
przez dwumiany 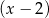 i
i 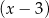 są odpowiednio równe
są odpowiednio równe 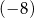 oraz
oraz 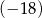 . Oblicz resztę z dzielenia wielomianu
. Oblicz resztę z dzielenia wielomianu 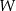 przez dwumian
przez dwumian 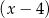 .
.
Dany jest graniastosłup prawidłowy trójkątny  . Krawędź podstawy tego graniastosłupa ma długość 4, a wysokość graniastosłupa jest równa 6 (zobacz rysunek).
. Krawędź podstawy tego graniastosłupa ma długość 4, a wysokość graniastosłupa jest równa 6 (zobacz rysunek).
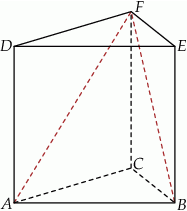
Oblicz sinus kąta 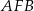 .
.
Czterowyrazowy ciąg 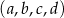 jest rosnący i arytmetyczny. Kwadrat największego wyrazu tego ciągu jest równy podwojonej sumie kwadratów pozostałych wyrazów tego ciągu. Ponadto ciąg
jest rosnący i arytmetyczny. Kwadrat największego wyrazu tego ciągu jest równy podwojonej sumie kwadratów pozostałych wyrazów tego ciągu. Ponadto ciąg 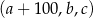 jest geometryczny. Oblicz wyrazy ciągu
jest geometryczny. Oblicz wyrazy ciągu 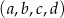 .
.
Dany jest równoległobok, którego boki zawierają się w prostych o równaniach: 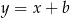 ,
, 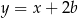 ,
, 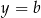 ,
, 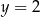 , gdzie liczba rzeczywista
, gdzie liczba rzeczywista 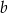 spełnia warunki:
spełnia warunki: 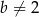 i
i 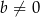 . Wyznacz wszystkie wartości parametru
. Wyznacz wszystkie wartości parametru 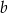 , dla których pole tego równoległoboku jest równe 1.
, dla których pole tego równoległoboku jest równe 1.
Wyznacz wszystkie wartości parametru  , dla których równanie
, dla których równanie 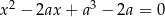 dwa różne rozwiązania dodatnie.
dwa różne rozwiązania dodatnie.
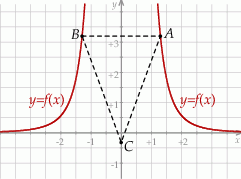
Rozpatrujemy wszystkie trójkąty 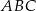 , których wierzchołki
, których wierzchołki 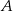 i
i 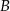 leżą na wykresie funkcji
leżą na wykresie funkcji 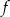 określonej wzorem
określonej wzorem 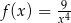 dla
dla 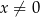 . Punkt
. Punkt 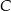 ma współrzędne
ma współrzędne 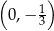 , a punkty
, a punkty 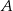 i
i 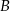 , są położone symetrycznie względem osi
, są położone symetrycznie względem osi 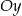 (zobacz rysunek). Oblicz współrzędne wierzchołków
(zobacz rysunek). Oblicz współrzędne wierzchołków 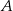 i
i 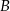 , dla których pole trójkąta
, dla których pole trójkąta 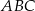 jest najmniejsze. Oblicz to najmniejsze pole.
jest najmniejsze. Oblicz to najmniejsze pole.