/Szkoła podstawowa/Egzamin ósmoklasisty/Egzamin 2021/Próbne testy
Próbny Egzamin Ósmoklasisty
z Matematyki Zestaw przygotowany przez serwis zadania.info 17 kwietnia 2021 Czas pracy: 100 minut
Podczas przeprowadzania ankiety na grupie 1100 osób zadano pytanie Z kim rozmawiałeś dziś przez telefon?. Wyniki ankiety przedstawiono na diagramie.
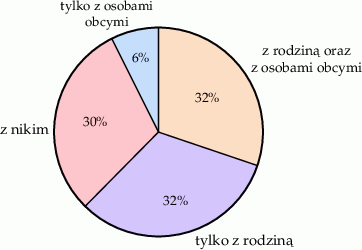
264 spośród ankietowanych osób nie odbyło rozmowy telefonicznej z powodu braku dostępu do telefonu. Ilu ankietowanych nie odbyło rozmowy telefonicznej z innego powodu? Zaznacz dobrą odpowiedź.
A) 836 B) 132 C) 330 D) 66
Dokończ zdanie. Zaznacz poprawną odpowiedź.
Liczbą podzielną przez 12 i 18 jest
A) 4734 B) 7212 C) 2484 D) 4944
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Liczbą mniejszą od 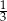 jest
jest
A) 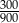 B)
B) 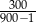 C)
C) 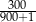 D)
D) 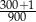
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Na osi liczbowej liczba równa wartości wyrażenia arytmetycznego 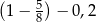 znajduje się między
znajduje się między
A) 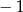 i
i 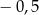 B)
B) 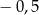 i 0 C) 0 i 0,5 D) 0,5 i 1
i 0 C) 0 i 0,5 D) 0,5 i 1
Tata Kamila przed wyjazdem z Warszawy do Krakowa analizuje niektóre bezpośrednie połączenia między tymi miastami. Do wyboru ma cztery połączenia przedstawione w poniższej tabeli.
| Godzina wyjazdu z Warszawy | Godzina przyjazdu do Krakowa | Środek transportu | Długość trasy | Cena biletu |
| 1:35 | 6:30 | autobus | 298 km | 27 zł |
| 2:32 | 5:12 | pociąg | 293 km | 60 zł |
| 4:36 | 8:48 | pociąg | 364 km | 58 zł |
| 5:53 | 8:10 | pociąg | 293 km | 65 zł |
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Za przejazd w najkrótszym czasie należy zapłacić 65 zł. | P | F |
| Zgodnie z rozkładem jazdy tylko przejazd autobusem trwa dłużej niż 4 godziny. | P | F |
W pudełku znajdują się kule w trzech kolorach. Kul niebieskich jest o 30 więcej niż kul zielonych, a kul czerwonych jest o 70 więcej niż kul niebieskich. Kule zielone i czerwone stanowią 75% wszystkich kul znajdujących się w pudełku. Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| W pudełku jest cztery razy więcej kul niebieskich niż zielonych. | P | F |
| W pudełku jest 40 kul niebieskich. | P | F |
Liczba 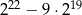 jest równa
jest równa
A) 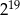 B)
B) 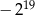 C)
C) 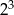 D)
D) 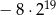
Liczba 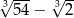 jest równa
jest równa
A) 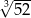 B) 3 C)
B) 3 C) 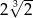 D) 2
D) 2
Na loterię przygotowano 500 losów, wśród których jest 40 losów wygrywających. Każdy los wygrywający upoważnia do odbioru nagrody w wysokości 15 zł. Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Pierwszych 17 losów zakupionych w loterii było przegrywających. Zuzia jako 18 osoba kupuje los w tej loterii. Prawdopodobieństwo, że los Zuzi jest wygrywający jest większe niż 0,08. | P | F |
| W drugiej edycji tej loterii zwiększono liczbę losów wygrywających dwukrotnie, a liczbę losów przegrywających pozostawiono bez zmian. Zatem prawdopodobieństwo wygranej wzrosło w drugiej edycji dwukrotnie. | P | F |
Jeżeli 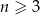 , to liczbę przekątnych wielokąta wypukłego o
, to liczbę przekątnych wielokąta wypukłego o  bokach można obliczyć ze wzoru
bokach można obliczyć ze wzoru
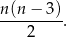
Uzupełnij zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
Wielokąt, który ma cztery razy więcej przekątnych niż boków ma A/B boków.
A) 10 B) 11
Liczba przekątnych wielokąta o 222 bokach jest liczbą C/D .
C) nieparzystą D) parzystą
Punkty 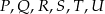 są środkami boków sześciokąta foremnego
są środkami boków sześciokąta foremnego  (rysunek).
(rysunek).
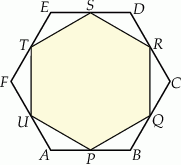
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Pole trójkąta  stanowi stanowi 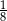 pola sześciokąta pola sześciokąta 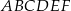 . . | P | F |
Pole sześciokąta 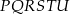 stanowi stanowi  pola sześciokąta pola sześciokąta 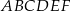 . . | P | F |
Na diagramie przedstawiono liczbę uczniów z podziałem na płeć w czterech klasach pewnej szkoły.
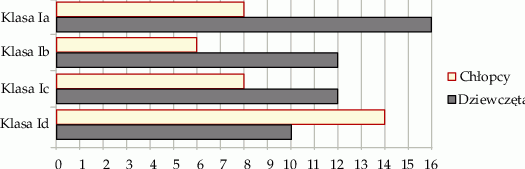
Czy wylosowanie dziewczynki jest bardziej prawdopodobne w klasie Ia, niż w każdej z trzech pozostałych klas? Wybierz odpowiedź T albo N i jej uzasadnienie spośród A, B albo C.
| Tak | Nie |
| ponieważ | |
| A) | w klasie Ia jest więcej dziewcząt, niż w każdej z pozostałych klas. |
| B) | stosunek liczby dziewcząt do liczby chłopców jest największy w klasie Ia. |
| C) | stosunek liczby dziewcząt do liczby chłopców jest taki sam w klasie Ia jak w jednej z pozostałych klas. |
Z kwadratowego kartonika odcięto naroża, tak jak pokazano na rysunku i otrzymano ośmiokąt foremny o bokach długości 2.
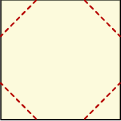
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Kartonik był kwadratem o polu 36. | P | F |
| Suma pól odciętych naroży jest równa 8. | P | F |
Przyprostokątne trójkąta prostokątnego mają długości 5 cm i 12 cm.
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Najkrótsza wysokość tego trójkąta ma długość
A) 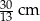 B) 5 cm C) 12 cm D)
B) 5 cm C) 12 cm D) 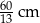
Oskar wykonał model prostopadłościanu. Układał i sklejał ze sobą kolejno drewniane klocki sześcienne o krawędzi 4 cm wzdłuż każdej ściany prostopadłościennego pudełka o wymiarach: 36 cm, 28 cm, 20 cm. Na rysunku przedstawiono część wykonanego modelu (model jest w środku pusty).
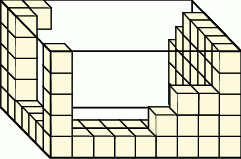
Ile klocków łącznie zużył Oskar na wykonanie całego modelu? Wybierz odpowiedź spośród podanych.
A) 315 B) 230 C) 246 D) 210
Jacek miał wziąć udział w obozie narciarskim, ale zachorował i zamiast niego na obóz pojechał jego dwa razy starszy brat. Ta zamiana spowodowała, że średnia wieku uczestników obozu wzrosła o rok. Oblicz, ile lat ma Jacek, jeżeli w obozie wzięło udział 12 osób. Zapisz obliczenia.
Z portu rybackiego (punkt  ) wypłynęły jednocześnie na połów dwa kutry: jeden na północ ze stałą prędkością 4 węzłów, drugi na wschód ze stałą prędkością 3 węzłów. Oblicz odległość między tymi kutrami po trzech godzinach od wypłynięcia. Wynik podaj w kilometrach. Zapisz obliczenia.
) wypłynęły jednocześnie na połów dwa kutry: jeden na północ ze stałą prędkością 4 węzłów, drugi na wschód ze stałą prędkością 3 węzłów. Oblicz odległość między tymi kutrami po trzech godzinach od wypłynięcia. Wynik podaj w kilometrach. Zapisz obliczenia.

Do rozwiązania zadania skorzystaj z informacji: 1 węzeł to 1 mila morska na godzinę, 1 mila morska = 1852 m.
Grupa motocyklistów w ciągu czterech dni pokonała dystans 221 km, przy czym liczby pokonanych kilometrów w kolejnych dniach są do siebie w proporcji 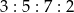 . Oblicz ile kilometrów motocykliści pokonywali w kolejnych dniach.
. Oblicz ile kilometrów motocykliści pokonywali w kolejnych dniach.
Boki trapezu równoramiennego mają długości 5 cm, 6 cm, 5 cm i 12 cm. Oblicz pole tego trapezu.

