/Szkoła podstawowa/Egzamin ósmoklasisty/Egzamin 2021/Próbne testy
Próbny Egzamin Ósmoklasisty
z Matematyki Zestaw przygotowany przez serwis zadania.info 8 maja 2021 Czas pracy: 100 minut
Tomek uczestniczył w czterodniowej wycieczce pieszej. W tabeli poniżej przedstawiono długości kolejnych etapów trasy, które przebył każdego dnia.
| Dzień | Długość kolejnych etapów trasy (w km) |
| wtorek | 24 |
| środa | 13 |
| czwartek | 15 |
| piątek | 20 |
Uzupełnij zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
W czwartek i piątek Tomek pokonał łącznie A/B długości całej trasy wycieczki.
A) więcej niż 50% B) mniej niż 50%
We wtorek Tomek przebył C/D długości całej trasy rajdu.
C) 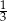 D)
D) 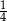
Która z liczb nie spełnia warunku 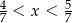 ?
?
Wybierz odpowiedź spośród podanych.
A) 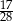 B)
B) 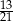 C)
C) 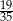 D)
D) 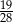
Trzy koleżanki - Kasia, Ala i Oliwia złożyły się na prezent urodzinowy dla ich wspólnego kolegi Kacpra. Prezent kosztował 225 zł, a kwoty wpłacone przez Kasię, Alę i Oliwię są – odpowiednio – w stosunku 4 : 5 : 6.
Jaką kwotę wpłaciła Ala? Wybierz odpowiedź spośród podanych.
A) 60 zł B) 75 zł C) 45 zł D) 90 zł
Ze zbioru kolejnych liczb naturalnych 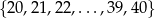 losujemy jedną liczbę. Prawdopodobieństwo wylosowania liczby podzielnej przez 4 jest równe
losujemy jedną liczbę. Prawdopodobieństwo wylosowania liczby podzielnej przez 4 jest równe
A) 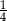 B)
B) 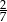 C)
C) 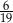 D)
D) 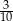
Liczba 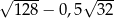 jest równa
jest równa
A) 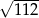 B)
B) 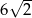 C)
C) 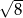 D)
D) 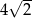
Pociąg o długości 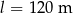 przejechał przez most o długości
przejechał przez most o długości 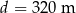 ze stałą prędkością
ze stałą prędkością 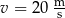 .
.
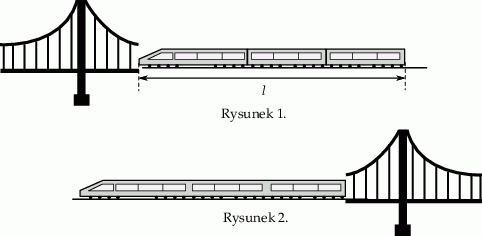
Ile czasu upłynęło od momentu wjazdu czoła pociągu na most (rysunek 1.) do momentu zjazdu z mostu końca ostatniego wagonu (rysunek 2.)?
Wybierz odpowiedź spośród podanych.
A) 6 s B) 16 s C) 25 s D) 22 s
Diagram przedstawia ile procent mieszkańców pewnego osiedla było w listopadzie w kinie 0,1,2,3 lub 4 razy. Średnia liczba wyjść do kina w listopadzie przypadających na jednego mieszkańca jest równa
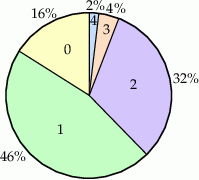
A) 1,3 B) 1,44 C) 2 D) 2,5
Która z podanych niżej liczb nie jest równa 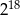 ? Wybierz właściwą odpowiedź spośród podanych.
? Wybierz właściwą odpowiedź spośród podanych.
A) 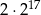 B)
B) 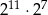 C)
C) 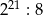 D)
D) 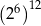 E)
E) 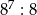
Na kartonowej siatce sześcianu Mariusz nakleił 6 figur tak, jak pokazano na rysunku. Następnie z tej siatki skleił kostkę.
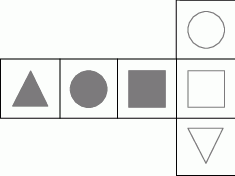
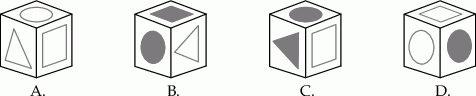
Który rysunek przedstawia kostkę sklejoną przez Mariusza? Wybierz właściwą odpowiedź spośród podanych.
Dany jest wzór opisujący pole trójkąta 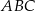 :
: 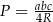 , gdzie
, gdzie 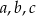 są długościami boków tego trójkąta, a
są długościami boków tego trójkąta, a 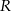 jest promieniem okręgu przechodzącego przez punkty
jest promieniem okręgu przechodzącego przez punkty 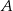 ,
, 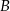 i
i 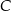 . Uzupełnij zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
. Uzupełnij zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
Promień 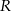 można wyrazić wzorem A/B .
można wyrazić wzorem A/B .
A) 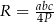 B)
B) 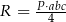
Długość boku  trójkąta
trójkąta 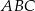 można wyrazić wzorem C/D .
można wyrazić wzorem C/D .
C) 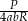 D)
D) 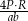
Kąt ostry rombu ma miarę 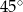 , a bok tego rombu ma długość równą 4 cm. Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
, a bok tego rombu ma długość równą 4 cm. Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Krótsza przekątna dzieli ten romb na dwa trójkąty prostokątne. | P | F |
Pole tego rombu jest równe 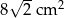 . . | P | F |
W układzie współrzędnych narysowano kwadrat o przekątnej długości 4 tak, że jednym z jego wierzchołków jest punkt 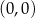 , a jedna z jego przekątnych jest równoległa do osi
, a jedna z jego przekątnych jest równoległa do osi 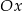 . Do tego kwadratu dorysowujemy kolejne takie same kwadraty. Umieszczamy je tak, jak na rysunku, aby każdy następny kwadrat miał z poprzednim dokładnie jeden wspólny wierzchołek oraz by jedna z przekątnych każdego kwadratu była równoległa do osi
. Do tego kwadratu dorysowujemy kolejne takie same kwadraty. Umieszczamy je tak, jak na rysunku, aby każdy następny kwadrat miał z poprzednim dokładnie jeden wspólny wierzchołek oraz by jedna z przekątnych każdego kwadratu była równoległa do osi 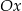 . Poniżej przedstawiono dorysowane, zgodnie z tą regułą, kwadraty, które ponumerowano kolejnymi liczbami naturalnymi.
. Poniżej przedstawiono dorysowane, zgodnie z tą regułą, kwadraty, które ponumerowano kolejnymi liczbami naturalnymi.
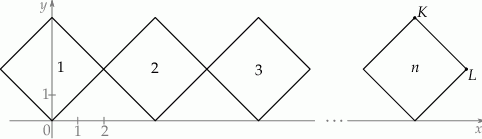
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Pierwsza współrzędna wierzchołka 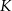 w w  –tym kwadracie jest równa –tym kwadracie jest równa 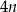 . . | P | F |
Pierwsza współrzędna wierzchołka 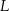 w w  –tym kwadracie jest równa –tym kwadracie jest równa 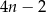 . . | P | F |
W październiku, w trzech hurtowniach budowlanych: Alfa, Beta i Gamma, sprzedawano styropian w tej samej cenie. Na wiosnę, w wyniku wzrostu kosztów produkcji styropianu, w każdym ze sklepów wywieszono informację o podwyżce. Poniżej przedstawiono oferty tych hurtowni.

Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Po podwyżce najniższa cena styropianu była w hurtowni Alfa. | P | F |
| Po podwyżce w jednej z hurtowni cena styropianu wzrosła o ponad 30 | P | F |
Na którym rysunku zamalowano 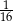 figury? Zaznacz poprawną odpowiedź.
figury? Zaznacz poprawną odpowiedź.

W trójkącie 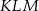 poprowadzono wysokość
poprowadzono wysokość 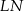 . Długości niektórych odcinków opisano za pomocą wyrażeń algebraicznych:
. Długości niektórych odcinków opisano za pomocą wyrażeń algebraicznych: 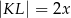 ,
, 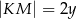 ,
, 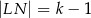 .
.
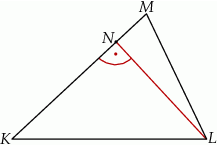
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Pole trójkąta 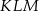 opisano wyrażeniem
opisano wyrażeniem
A) 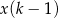 B)
B) 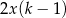 C)
C) 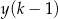 D)
D) 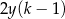
Trasa rowerowa wokół jeziora ma długość 15 km. Dwóch rowerzystów wyrusza z tego samego miejsca i okrąża jezioro poruszając się w tym samym kierunku. Średnia prędkość drugiego z nich jest większa od średniej prędkości pierwszego o 5 km/h. Oblicz po jakim czasie dojdzie do ponownego spotkania rowerzystów.
Właściciel sklepu sportowego kupił w hurtowni deskorolki i kaski. Cena hurtowa deskorolki była o 60 zł wyższa niż cena hurtowa kasku. Właściciel sklepu ustalił cenę sprzedaży deskorolki o 20% wyższą od ceny hurtowej, a cenę sprzedaży kasku – o 40% wyższą od ceny hurtowej. Deskorolka i kask łącznie kosztowały w sklepie 397 zł. Oblicz łączny koszt zakupu po cenach hurtowych jednej deskorolki i jednego kasku. Zapisz obliczenia.
Na rysunku przedstawiono układ miejsc w przedziale sześcioosobowym wagonu kolejowego i zaznaczono kierunek jazdy pociągu.
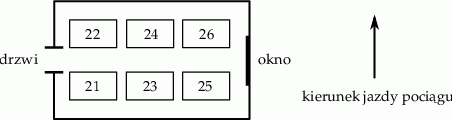
Krzysiek i Antek planują zakup biletów na wspólną podróż. Wszystkie miejsca w przedziale są wolne. Krzysiek chce siedzieć przodem do kierunku jazdy, natomiast Antek chce siedzieć przy oknie lub przy drzwiach, ale nie chce siedzieć naprzeciwko Krzyśka. Podaj wszystkie możliwości wyboru miejsc spełniające jednocześnie powyższe warunki.
Oblicz pole i obwód trapezu prostokątnego przedstawionego na rysunku.