/Szkoła średnia/Zadania maturalne/Matura 2022
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis zadania.info poziom podstawowy 19 marca 2022 Czas pracy: 170 minut
Zadania zamknięte
Liczba 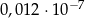 jest równa
jest równa
A) 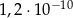 B)
B) 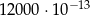 C)
C) 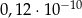 D) 0,00000012
D) 0,00000012
Liczba 1371,37 jest o 37% większa od 44% połowy liczby  . Wtedy liczba
. Wtedy liczba  jest równa
jest równa
A) 9100 B) 2275 C) 4550 D) 5148
Liczba 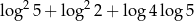 jest
jest
A) dodatnia B) mniejsza od 1 C) ujemna D) niewymierna
Dla każdych liczb rzeczywistych  i
i 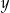 wyrażenie
wyrażenie 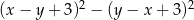 jest równe
jest równe
A) 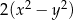 B)
B) 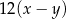 C)
C) 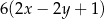 D) 9
D) 9
Liczba 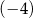 jest rozwiązaniem równania
jest rozwiązaniem równania
A) 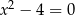 B)
B) 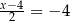 C)
C) 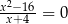 D)
D) 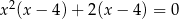
Zbiorem wszystkich rozwiązań nierówności 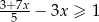 jest przedział
jest przedział
A) 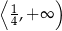 B)
B) 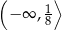 C)
C) 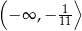 D)
D) 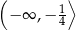
Rozwiązaniem równania 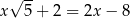 jest liczba
jest liczba
A) 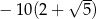 B)
B) 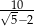 C)
C) 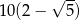 D)
D) 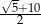
Przedział 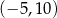 jest zbiorem rozwiązań nierówności
jest zbiorem rozwiązań nierówności
A) 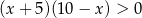 B)
B) 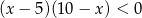
C) 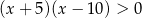 D)
D) 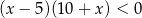
Prosta 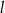 tworzy z osią
tworzy z osią 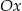 kąt ostry
kąt ostry 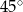 (zobacz rysunek) oraz przechodzi przez punkt o współrzędnych
(zobacz rysunek) oraz przechodzi przez punkt o współrzędnych 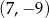 .
.
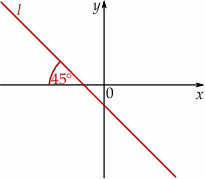
Prosta 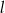 ma równanie
ma równanie
A) 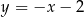 B)
B) 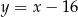 C)
C) 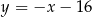 D)
D) 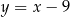
Funkcja 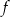 jest określona wzorem
jest określona wzorem 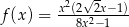 . Wtedy dla argumentu
. Wtedy dla argumentu 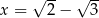 wartość funkcji
wartość funkcji 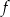 jest równa
jest równa
A) 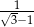 B)
B) 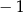 C) 1 D)
C) 1 D) 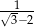
Ciąg arytmetyczny 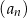 jest określony dla każdej liczby naturalnej
jest określony dla każdej liczby naturalnej 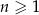 . Różnica tego ciągu jest równa
. Różnica tego ciągu jest równa 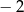 . Wtedy
. Wtedy
A) 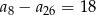 B)
B) 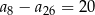 C)
C) 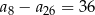 D)
D) 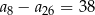
Ciąg 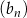 jest określony wzorem
jest określony wzorem 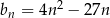 dla każdej liczby naturalnej
dla każdej liczby naturalnej 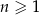 . Liczba niedodatnich wyrazów ciągu
. Liczba niedodatnich wyrazów ciągu 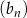 jest równa
jest równa
A) 6 B) 12 C) 9 D) 8
Informacja do zadań 13 i 14
Funkcja kwadratowa 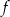 jest określona wzorem
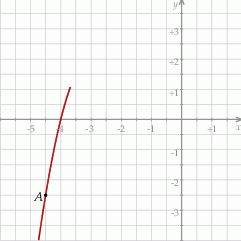
jest określona wzorem 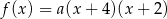 . Na rysunku przedstawiono fragment paraboli będącej wykresem tej funkcji. Jednym z punktów tej paraboli jest punkt
. Na rysunku przedstawiono fragment paraboli będącej wykresem tej funkcji. Jednym z punktów tej paraboli jest punkt 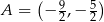 .
.
Współczynnik  we wzorze funkcji
we wzorze funkcji 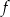 jest równy
jest równy
A) 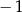 B)
B) 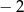 C) 2 D) 1
C) 2 D) 1
Najmniejsza wartość funkcji 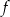 w przedziale
w przedziale 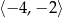 jest równa
jest równa
A) 0 B) 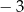 C)
C) 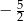 D)
D) 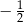
Układ równań 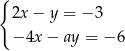 opisuje w układzie współrzędnych zbiór pusty dla
opisuje w układzie współrzędnych zbiór pusty dla
A) 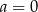 B)
B) 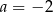 C)
C) 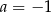 D)
D) 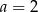
W ciągu geometrycznym 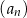 , określonym dla
, określonym dla 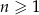 , dane są:
, dane są: 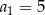 ,
, 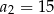 . Wtedy
. Wtedy
A) 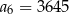 B)
B) 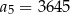 C)
C) 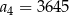 D)
D) 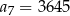
Na poniższym rysunku punkt 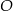 jest środkiem okręgu.
jest środkiem okręgu.
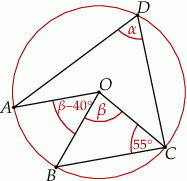
Miara kąta  jest równa
jest równa
A)  B)
B) 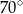 C)
C) 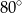 D)
D) 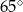
Przeciwprostokątna 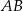 trójkąta prostokątnego
trójkąta prostokątnego 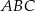 ma długość 26, a pole tego trójkąta jest równe 120 (zobacz rysunek).
ma długość 26, a pole tego trójkąta jest równe 120 (zobacz rysunek).
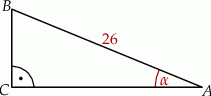
Jeżeli  jest najmniejszym z kątów wewnętrznych tego trójkąta, to wartość wyrażenia
jest najmniejszym z kątów wewnętrznych tego trójkąta, to wartość wyrażenia 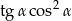 jest równa
jest równa
A) 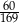 B)
B) 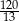 C)
C) 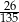 D)
D) 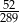
Punkt 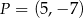 przekształcono w symetrii względem symetralnej odcinka o końcach
przekształcono w symetrii względem symetralnej odcinka o końcach 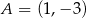 i
i 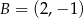 . W wyniku tego przekształcenia otrzymano punkt
. W wyniku tego przekształcenia otrzymano punkt 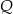 . Zatem długość odcinka
. Zatem długość odcinka 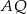 jest równa
jest równa
A) 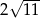 B)
B) 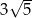 C)
C) 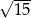 D)
D) 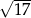
W układzie współrzędnych dane są dwa punkty 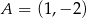 oraz
oraz 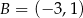 . Współczynnik kierunkowy prostej
. Współczynnik kierunkowy prostej 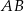 jest równy
jest równy
A) 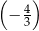 B)
B) 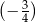 C)
C)  D)
D) 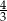
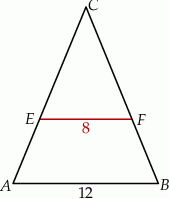
W trójkącie równoramiennym 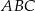 dane są
dane są 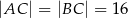 oraz
oraz 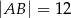 . Odcinek
. Odcinek 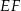 jest równoległy do podstawy
jest równoległy do podstawy 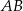 oraz
oraz 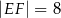 . Długość odcinka
. Długość odcinka 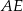 jest równa
jest równa
A) 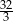 B)
B)  C)
C) 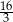 D)
D) 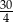
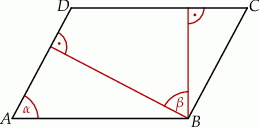
W równoległoboku 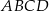 , przedstawionym na rysunku, kąt
, przedstawionym na rysunku, kąt  ma miarę
ma miarę 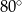 .
.
Wtedy kąt 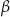 ma miarę
ma miarę
A) 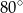 B)
B) 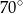 C)
C) 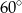 D)
D) 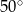
W prostokącie 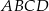 dane są wierzchołki
dane są wierzchołki 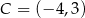 oraz
oraz 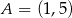 . Bok
. Bok 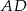 ma długość 3. Pole tego prostokąta jest równe
ma długość 3. Pole tego prostokąta jest równe
A) 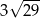 B)
B) 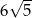 C) 24 D) 18
C) 24 D) 18
Pole działki budowlanej jest równe 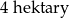 . Pole powierzchni tej działki na planie wykonanym w skali 1:200 wynosi:
. Pole powierzchni tej działki na planie wykonanym w skali 1:200 wynosi:
A) 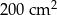 B)
B) 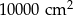 C)
C) 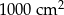 D)
D) 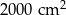
Ile jest liczb naturalnych czterocyfrowych o różnych cyfrach, których iloczyn cyfr jest równy 0?
A) 1728 B) 504 C) 720 D) 1512
Z wierzchołków sześciokąta foremnego 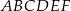 losujemy jednocześnie dwa różne wierzchołki. Prawdopodobieństwo tego, że wierzchołki te będą końcami przekątnej sześciokąta
losujemy jednocześnie dwa różne wierzchołki. Prawdopodobieństwo tego, że wierzchołki te będą końcami przekątnej sześciokąta 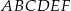 jest równe
jest równe
A) 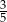 B)
B) 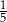 C)
C) 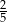 D)
D) 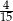
Suma długości wszystkich przekątnych sześcianu jest równa 24. Pole powierzchni całkowitej tego sześcianu jest równe
A) 144 B) 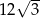 C) 36 D) 72
C) 36 D) 72
Średnia arytmetyczna liczb: 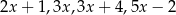 i
i 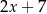 zmniejsza się o 1 jeżeli pominiemy ostatnią liczbę. Wynika stąd, że
zmniejsza się o 1 jeżeli pominiemy ostatnią liczbę. Wynika stąd, że
A) 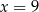 B)
B) 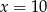 C)
C) 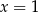 D)
D) 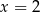
Zadania otwarte
Rozwiąż nierówność 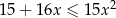 .
.
Wykaż, że dla każdych trzech liczb 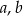 i
i  takich, że
takich, że 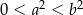 i
i 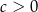 spełniona jest nierówność
spełniona jest nierówność
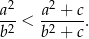
Na rysunku przedstawiono bryłę, której podstawą jest kwadrat a ściany boczne są prostopadłe do płaszczyzny podstawy. Wymiary bryły podane są na rysunku.
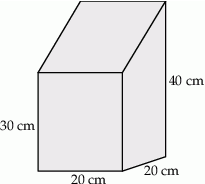
Oblicz objętość tej bryły.
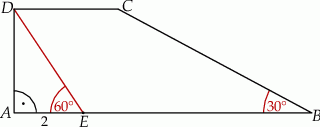
W trapezie prostokątnym 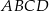 krótsze ramię
krótsze ramię 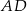 i krótsza podstawa
i krótsza podstawa 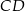 mają tę samą długość oraz
mają tę samą długość oraz 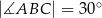 . Na podstawie
. Na podstawie 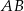 wybrano punkt
wybrano punkt 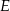 tak, że
tak, że 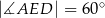 oraz
oraz 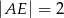 (zobacz rysunek). Oblicz długość odcinka
(zobacz rysunek). Oblicz długość odcinka 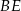 .
.
Okrąg wpisany w trójkąt równoboczny 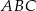 jest jednocześnie okręgiem opisanym na trójkącie równobocznym
jest jednocześnie okręgiem opisanym na trójkącie równobocznym 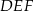 . O ile procent pole trójkąta
. O ile procent pole trójkąta 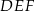 jest mniejsze od pola trójkąta
jest mniejsze od pola trójkąta 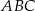 ?
?
Rzucamy trzy razy symetryczną sześcienną kostką do gry. Oblicz prawdopodobieństwo zdarzenia 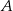 polegającego na tym, że suma liczb wyrzuconych oczek nie jest równa 4.
polegającego na tym, że suma liczb wyrzuconych oczek nie jest równa 4.
Każdy z wierzchołków trójkąta prostokątnego 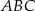 leży na na wykresie funkcji
leży na na wykresie funkcji 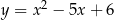 . Bok
. Bok 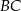 tego trójkąta jest zawarty w prostej
tego trójkąta jest zawarty w prostej 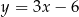 , a wierzchołek
, a wierzchołek 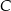 kąta prostego ma obie współrzędne dodatnie. Oblicz pole trójkąta
kąta prostego ma obie współrzędne dodatnie. Oblicz pole trójkąta 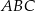 .
.

