/Szkoła średnia/Zadania maturalne/Matura 2022
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis zadania.info poziom podstawowy 26 lutego 2022 Czas pracy: 170 minut
Zadania zamknięte
Andrzej połowę kwoty otrzymanej od taty przeznaczył na nową kurtkę, a 20% tego, co mu pozostało przeznaczył na bilet do kina. Ile procent kwoty otrzymanej od taty pozostało Andrzejowi?
A) 30% B) 80% C) 40% D) 20%
Liczba 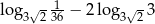 jest równa
jest równa
A) 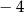 B)
B) 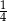 C) 4 D)
C) 4 D) 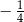
Rozważamy przedziały liczbowe 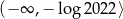 i
i 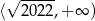 . Ile jest wszystkich liczb całkowitych, które nie należą do żadnego z tych przedziałów?
. Ile jest wszystkich liczb całkowitych, które nie należą do żadnego z tych przedziałów?
A) 48 B) 44 C) 46 D) 43
Liczba 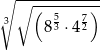 jest równa
jest równa
A) 4 B) 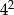 C)
C) 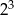 D) 2
D) 2
W rozwinięciu dziesiętnym ułamka 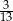 na trzydziestym miejscu po przecinku stoi cyfra
na trzydziestym miejscu po przecinku stoi cyfra
A) 6 B) 9 C) 2 D) 3
Zbiorem wszystkich rozwiązań nierówności 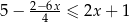 jest przedział
jest przedział
A) 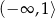 B)
B) 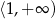 C)
C) 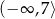 D)
D) 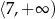
Na poniższym rysunku przedstawiono wykres funkcji 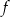 określonej w zbiorze
określonej w zbiorze 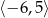 .
.
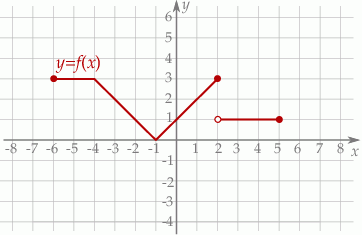
Funkcja 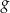 jest określona wzorem
jest określona wzorem 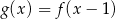 dla
dla 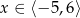 . Wskaż zdanie prawdziwe.
. Wskaż zdanie prawdziwe.
A) Liczba 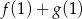 jest równa 2.
jest równa 2.
B) Zbiory wartości funkcji 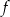 i
i 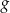 są równe.
są równe.
C) Funkcje 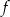 i
i 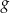 mają takie same miejsca zerowe.
mają takie same miejsca zerowe.
D) Punkt 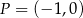 należy do wykresów funkcji
należy do wykresów funkcji 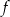 i
i 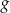 .
.
Równanie 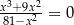 ma w zbiorze liczb rzeczywistych dokładnie
ma w zbiorze liczb rzeczywistych dokładnie
A) jedno rozwiązanie. B) dwa rozwiązania.
C) trzy rozwiązania. D) cztery rozwiązania.
Funkcja 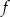 jest określona dla każdej liczby rzeczywistej
jest określona dla każdej liczby rzeczywistej  wzorem
wzorem 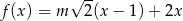 . Ta funkcja jest rosnąca dla każdej liczby
. Ta funkcja jest rosnąca dla każdej liczby 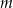 spełniającej warunek
spełniającej warunek
A) 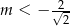 B)
B) 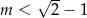 C)
C) 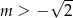 D)
D) 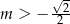
Funkcja kwadratowa 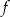 jest określona wzorem
jest określona wzorem 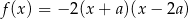 . Wierzchołek paraboli, która jest wykresem funkcji
. Wierzchołek paraboli, która jest wykresem funkcji 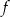 , ma współrzędną
, ma współrzędną 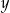 równą 2. Zatem liczba
równą 2. Zatem liczba  może być równa
może być równa
A) 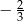 B)
B)  C) 4 D)
C) 4 D) 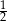
Punkt 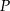 jest punktem wspólnym wykresu funkcji
jest punktem wspólnym wykresu funkcji 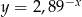 i prostej
i prostej 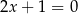 . Odległość punktu
. Odległość punktu 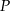 od osi
od osi 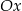 układu współrzędnych jest równa
układu współrzędnych jest równa
A) 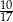 B)
B) 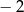 C) 1,7 D) 1
C) 1,7 D) 1
Wartość wyrażenia 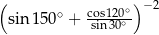 jest równa
jest równa
A) 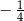 B) 4 C) 1 D)
B) 4 C) 1 D) 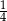
Dane są ciągi 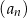 ,
, 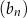 ,
, 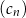 ,
, 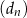 , określone dla każdej liczby naturalnej
, określone dla każdej liczby naturalnej 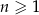 wzorami:
wzorami: 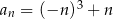 ,
, 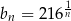 ,
, 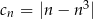 ,
, 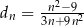 . Dodatnia liczba całkowita dwucyfrowa jest trzecim wyrazem ciągu
. Dodatnia liczba całkowita dwucyfrowa jest trzecim wyrazem ciągu
A) 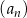 B)
B) 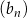 C)
C) 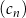 D)
D) 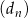
Dany jest odcinek 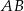 , gdzie
, gdzie 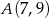 ,
, 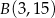 . Punkt
. Punkt 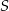 jest środkiem odcinka
jest środkiem odcinka 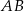 . Obrazem punktu
. Obrazem punktu 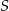 w symetrii względem osi
w symetrii względem osi 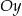 jest punkt
jest punkt
A) 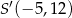 B)
B) 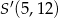 C)
C) 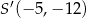 D)
D) 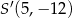
Ciąg arytmetyczny 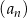 jest określony dla każdej liczby naturalnej
jest określony dla każdej liczby naturalnej 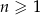 . Trzeci i piąty wyraz ciągu spełniają warunek
. Trzeci i piąty wyraz ciągu spełniają warunek 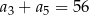 . Wtedy czwarty wyraz tego ciągu jest równy
. Wtedy czwarty wyraz tego ciągu jest równy
A) 28 B) 29 C) 33 D) 40
Trójwyrazowy ciąg 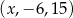 jest ciągiem geometrycznym. Wtedy
jest ciągiem geometrycznym. Wtedy
A) 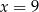 B)
B) 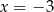 C)
C) 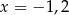 D)
D) 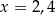
Pole pewnego sześciokąta foremnego jest równe 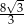 . Obwód tego sześciokąta jest równy
. Obwód tego sześciokąta jest równy
A) 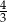 B) 8 C) 4 D) 12
B) 8 C) 4 D) 12
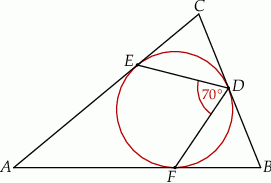
Dane są okrąg i prosta styczna do tego okręgu w punkcie 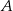 . Punkty
. Punkty 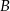 i
i 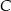 są położone na okręgu tak, że
są położone na okręgu tak, że 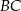 jest jego średnicą. Cięciwa
jest jego średnicą. Cięciwa 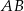 tworzy ze styczną kąt o mierze
tworzy ze styczną kąt o mierze 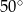 (zobacz rysunek).
(zobacz rysunek).
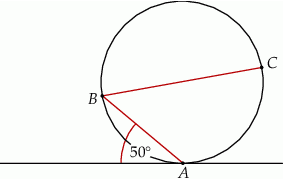
Miara kąta 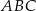 jest równa
jest równa
A) 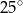 B)
B) 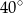 C)
C) 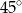 D)
D) 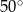
Punkty 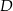 ,
, 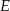 i
i 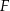 są punktami styczności okręgu wpisanego w trójkąt
są punktami styczności okręgu wpisanego w trójkąt 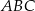 z jego bokami i
z jego bokami i 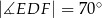 (zobacz rysunek).
(zobacz rysunek).
Miara kąta 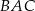 jest równa
jest równa
A) 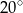 B)
B) 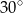 C)
C) 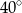 D)
D) 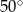
Jeśli 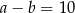 oraz
oraz 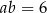 , to
, to 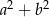 jest równe
jest równe
A) 122 B) 106 C) 94 D) 112
Punkty 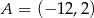 ,
, 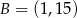 i
i 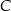 leżą na jednej prostej. Punkt
leżą na jednej prostej. Punkt 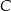 może mieć współrzędne
może mieć współrzędne
A) 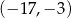 B)
B) 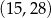 C)
C) 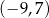 D)
D) 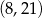
W każdym  –kącie wypukłym (
–kącie wypukłym (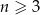 ) liczba przekątnych jest równa
) liczba przekątnych jest równa 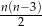 . Wielokątem wypukłym, w którym liczba przekątnych jest o 33 większa od liczby boków, jest
. Wielokątem wypukłym, w którym liczba przekątnych jest o 33 większa od liczby boków, jest
A) dziewięciokąt. B) jedenastokąt. C) dziesięciokąt. D) piętnastokąt.
Prosta 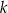 ma równanie
ma równanie 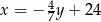 . Współczynnik kierunkowy prostej prostopadłej do prostej
. Współczynnik kierunkowy prostej prostopadłej do prostej 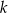 jest równy
jest równy
A)  B)
B) 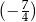 C)
C) 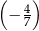 D)
D) 
Okrąg o środku 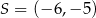 jest styczny do osi
jest styczny do osi 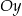 układu współrzędnych w punkcie
układu współrzędnych w punkcie 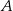 oraz jest styczny do prostej
oraz jest styczny do prostej 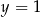 w punkcie
w punkcie 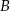 . Promień okręgu o średnicy
. Promień okręgu o średnicy 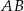 jest równy
jest równy
A) 6 B) 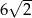 C) 12 D)
C) 12 D) 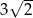
Przekątna graniastosłupa prawidłowego czworokątnego, w którym wysokość jest 2 razy dłuższa od krawędzi podstawy, jest równa 6. Wynika stąd, że objętość tego graniastosłupa jest równa
A) 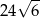 B)
B) 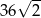 C)
C) 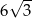 D)
D) 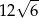
W tabeli podano dane dotyczące wyników z pracy klasowej z matematyki uzyskanych w pewnej klasie.
| Liczba uczniów | 5 | 3 | 5 | 7 | 3 | 1 |
| Ocena | 1 | 2 | 3 | 4 | 5 | 6 |
Różnica średniej arytmetycznej ocen i mediany wynosi
A) 3,125 B)  C) 1,125 D)
C) 1,125 D) 
Ile jest liczb naturalnych trzycyfrowych większych od 694, które mają trzy różne cyfry?
A) 216 B) 219 C) 221 D) 246
W pudełku znajdują się płytki z literami. Na każdej płytce jest wydrukowana jedna litera – spółgłoskowa albo samogłoskowa. Płytek z literami spółgłoskowymi jest o 40% więcej niż płytek z literami samogłoskowymi. Losujemy jedną płytkę. Prawdopodobieństwo wylosowania płytki z literą samogłoskową jest równe
A) 0,6 B) 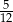 C)
C)  D) 0,4
D) 0,4
Zadania otwarte
Rozwiąż nierówność: 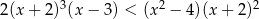 .
.
Rozwiąż równanie 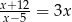 .
.
Funkcja liniowa 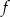 przyjmuje wartość 2 dla argumentu
przyjmuje wartość 2 dla argumentu 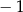 , a ponadto
, a ponadto 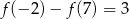 . Wyznacz wzór funkcji
. Wyznacz wzór funkcji 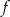 .
.
Wykaż, że jeżeli  jest parzystą liczbą całkowitą dodatnią, to liczba
jest parzystą liczbą całkowitą dodatnią, to liczba 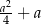 nie jest kwadratem liczby całkowitej.
nie jest kwadratem liczby całkowitej.
Na bokach 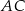 i
i 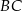 trójkąta
trójkąta 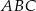 wybrano odpowiednio punkty
wybrano odpowiednio punkty 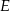 i
i 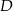 w ten sposób, że
w ten sposób, że 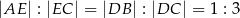 . Punkt
. Punkt 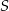 jest punktem wspólnym odcinków
jest punktem wspólnym odcinków 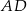 i
i 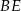 (zobacz rysunek).
(zobacz rysunek).
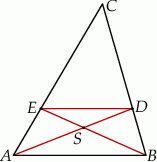
Oblicz pole trójkąta 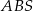 jeżeli pole trójkąta
jeżeli pole trójkąta 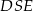 równe 36.
równe 36.
Ze zbioru wszystkich liczb naturalnych dwucyfrowych, których cyfra dziesiątek należy do zbioru 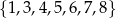 , a cyfra jedności należy do zbioru
, a cyfra jedności należy do zbioru 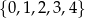 , losujemy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że wylosujemy liczbę dwucyfrową, która jest podzielna przez 8.
, losujemy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że wylosujemy liczbę dwucyfrową, która jest podzielna przez 8.
Punkty 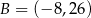 ,
, 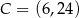 i
i 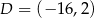 są wierzchołkami trapezu równoramiennego
są wierzchołkami trapezu równoramiennego 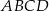 o podstawach
o podstawach 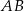 i
i 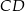 . Wyznacz współrzędne wierzchołka
. Wyznacz współrzędne wierzchołka 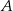 tego trapezu jeżeli wiadomo, że
tego trapezu jeżeli wiadomo, że 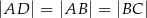 .
.

