/Szkoła średnia/Zadania maturalne/Matura 2022
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis zadania.info poziom rozszerzony 19 marca 2022 Czas pracy: 180 minut
Zadania zamknięte
Odległość liczby  od liczby
od liczby 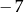 na osi liczbowej jest równa
na osi liczbowej jest równa
A) 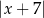 B)
B) 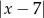 C)
C) 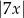 D)
D) 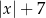
Granice 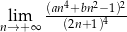 i
i 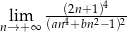 są równe. Stąd wynika, że
są równe. Stąd wynika, że
A) 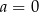 i
i 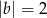 B)
B) 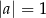 i
i 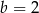 C)
C) 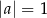 i
i 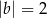 D)
D) 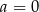 i
i 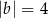
Na rysunku przedstawiono fragment wykresu funkcji 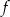 określonej dla każdej liczby rzeczywistej
określonej dla każdej liczby rzeczywistej  .
.
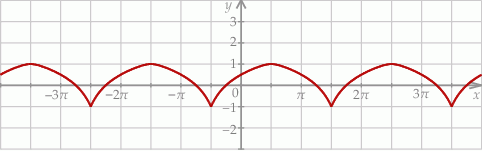
Jeden spośród podanych poniżej wzorów jest wzorem tej funkcji. Wskaż wzór funkcji 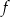 .
.
A) 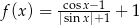 B)
B) 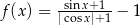
C) 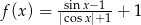 D)
D) 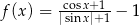
Suma szeregu geometrycznego 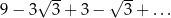 jest równa
jest równa
A) 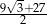 B)
B) 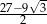 C)
C) 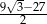 D)
D) 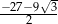
Zadania otwarte
Reszta z dzielenia wielomianu 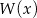 przez
przez 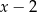 jest równa 7. Oblicz resztę z dzielenia wielomianu
jest równa 7. Oblicz resztę z dzielenia wielomianu 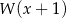 przez wielomian
przez wielomian 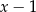 .
.
Niech 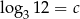 . Wykaż, że
. Wykaż, że 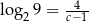 .
.
Dany jest trójkąt 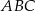 . Na boku
. Na boku 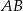 tego trójkąta obrano punkty
tego trójkąta obrano punkty 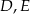 i
i 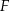 tak, że
tak, że 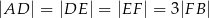 . Na bokach
. Na bokach 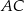 i
i 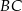 obrano – odpowiednio – punkty
obrano – odpowiednio – punkty 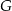 i
i 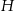 tak, że
tak, że 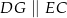 oraz
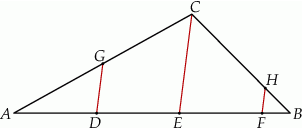
oraz 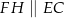 (zobacz rysunek). Wykaż, że jeżeli pole trójkąta
(zobacz rysunek). Wykaż, że jeżeli pole trójkąta 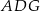 jest równe
jest równe 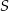 , to pole trójkąta
, to pole trójkąta 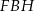 jest równe
jest równe 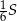 .
.
Liczby 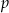 i
i 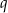 są pierwiastkami równania
są pierwiastkami równania 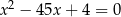 . Wykaż, że wartość wyrażenia
. Wykaż, że wartość wyrażenia
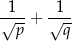
jest liczbą wymierną.
Wykaż, że wszystkie trójkąty ograniczone osiami układu współrzędnych i dowolną styczną do wykresu funkcji 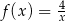 , określonej dla
, określonej dla 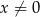 , mają równe pola.
, mają równe pola.
Dane są dwa okręgi o równaniach 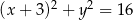 i
i 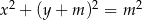 ,
, 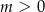 . Wyznacz wszystkie wartości parametru
. Wyznacz wszystkie wartości parametru 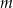 , dla których te okręgi mają jeden punkt wspólny.
, dla których te okręgi mają jeden punkt wspólny.
W pewnym wagonie kolejowym pasażerowie siadają w sposób losowy na 54 siedzeniach, które są ustawione po trzy siedzenia w jednym rzędzie. Do wagonu wsiadło o 3 pasażerów mniej niż dostępna liczba siedzeń i dokładnie troje z tych pasażerów to mężczyźni. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że mężczyźni usiedli w jednym rzędzie i jednocześnie jeden cały rząd pozostał pusty.
Wyznacz wszystkie liczby rzeczywiste 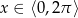 , które spełniają równanie
, które spełniają równanie
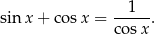
Na okręgu jest opisany czworokąt 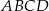 . Bok
. Bok 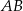 tego czworokąta jest trzy razy krótszy od przekątnej
tego czworokąta jest trzy razy krótszy od przekątnej 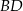 , a bok
, a bok 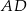 ma długość 10. Ponadto spełnione są następujące warunki:
ma długość 10. Ponadto spełnione są następujące warunki:
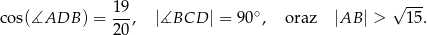
Oblicz długość boku 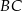 tego czworokąta.
tego czworokąta.
Krótsza przekątna graniastosłupa prawidłowego sześciokątnego tworzy z płaszczyzną podstawy kąt 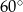 . Przekątna ściany bocznej ma długość
. Przekątna ściany bocznej ma długość 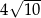 .
.
- Oblicz objętość i pole powierzchni całkowitej tego graniastosłupa.
- Oblicz cosinus kąta między krótszymi przekątnymi graniastosłupa wychodzącymi z jednego wierzchołka.
Dany jest trójkąt równoboczny 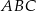 o boku długości
o boku długości  . Punkty
. Punkty 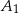 ,
, 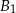 i
i 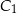 należą do boków
należą do boków 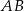 ,
, 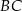 i
i 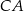 , przy czym
, przy czym 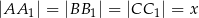 .
.
- Wyraź pole trójkąta
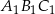 jako funkcję zmiennej
jako funkcję zmiennej  . Wyznacz dziedzinę tej funkcji.
. Wyznacz dziedzinę tej funkcji. - Wyznacz wartość
 , dla której pole trójkąta
, dla której pole trójkąta 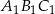 jest najmniejsze. Oblicz to najmniejsze pole.
jest najmniejsze. Oblicz to najmniejsze pole.

