/Szkoła średnia/Zadania maturalne/Matura 2022
Egzamin Maturalny
z Matematyki poziom rozszerzony 11 maja 2022 Czas pracy: 180 minut
Zadania zamknięte
Liczba 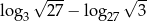 jest równa
jest równa
A) 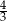 B)
B) 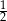 C)
C) 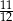 D) 3
D) 3
Funkcja 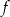 jest określona wzorem
jest określona wzorem 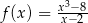 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej 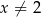 . Wartość pochodnej tej funkcji dla argumentu
. Wartość pochodnej tej funkcji dla argumentu 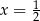 jest równa
jest równa
A)  B)
B)  C) 3 D)
C) 3 D) 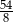
Jeżeli 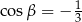 i
i 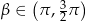 , to wartość wyrażenia
, to wartość wyrażenia 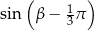 jest równa
jest równa
A) 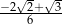 B)
B) 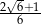 C)
C) 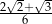 D)
D) 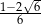
Dane są dwie urny z kulami. W każdej z urn jest siedem kul. W pierwszej urnie są jedna kula biała i sześć kul czarnych, w drugiej urnie są cztery kule białe i trzy kule czarne. Rzucamy jeden raz symetryczną monetą. Jeżeli wypadnie reszka, to losujemy jedną kulę z pierwszej urny, w przeciwnym przypadku – jedną kulę z drugiej urny. Prawdopodobieństwo zdarzenia polegającego na tym, że wylosujemy kulę białą w tym doświadczeniu, jest równe
A) 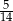 B)
B) 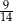 C)
C) 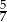 D)
D) 
Zadania otwarte
Ciąg 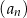 jest określony dla każdej liczby naturalnej
jest określony dla każdej liczby naturalnej 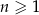 wzorem
wzorem
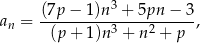
gdzie 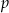 jest liczbą rzeczywistą dodatnią. Oblicz wartość
jest liczbą rzeczywistą dodatnią. Oblicz wartość 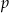 , dla której granica ciągu
, dla której granica ciągu 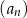 jest równa
jest równa 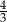 .
.
Wykaż, że dla każdej liczby rzeczywistej  i dla każdej liczby rzeczywistej
i dla każdej liczby rzeczywistej 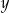 takich, że
takich, że 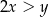 , spełniona jest nierówność
, spełniona jest nierówność
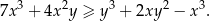
Rozwiąż równanie 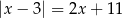 .
.
Punkt 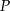 jest punktem przecięcia przekątnych trapezu
jest punktem przecięcia przekątnych trapezu 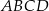 . Długość podstawy
. Długość podstawy 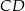 jest o 2 mniejsza od długości podstawy
jest o 2 mniejsza od długości podstawy 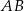 . Promień okręgu opisanego na trójkącie ostrokątnym
. Promień okręgu opisanego na trójkącie ostrokątnym 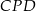 jest o 3 mniejszy od promienia okręgu opisanego na trójkącie
jest o 3 mniejszy od promienia okręgu opisanego na trójkącie 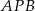 . Wykaż, że spełniony jest warunek
. Wykaż, że spełniony jest warunek 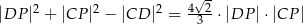 .
.
Reszta z dzielenia wielomianu 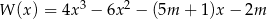 przez dwumian
przez dwumian 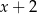 jest równa
jest równa 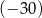 . Oblicz
. Oblicz 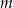 i dla wyznaczonej wartości
i dla wyznaczonej wartości 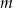 rozwiąż nierówność
rozwiąż nierówność 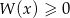 .
.
Ciąg 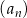 , określony dla każdej liczby naturalnej
, określony dla każdej liczby naturalnej 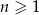 , jest geometryczny i ma wszystkie wyrazy dodatnie. Ponadto
, jest geometryczny i ma wszystkie wyrazy dodatnie. Ponadto 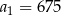 i
i 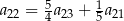 . Ciąg
. Ciąg 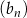 , określony dla każdej liczby naturalnej
, określony dla każdej liczby naturalnej 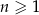 , jest arytmetyczny. Suma wszystkich wyrazów ciągu
, jest arytmetyczny. Suma wszystkich wyrazów ciągu 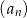 jest równa sumie dwudziestu pięciu początkowych kolejnych wyrazów ciągu
jest równa sumie dwudziestu pięciu początkowych kolejnych wyrazów ciągu 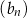 . Ponadto
. Ponadto 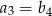 . Oblicz
. Oblicz 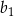 .
.
Rozwiąż równanie 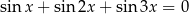 w przedziale
w przedziale 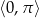 .
.
Wyznacz wszystkie wartości parametru 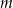 , dla których równanie
, dla których równanie
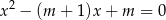
ma dwa różne rozwiązania rzeczywiste 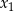 oraz
oraz 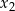 , spełniające warunki:
, spełniające warunki:
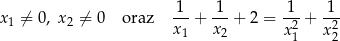
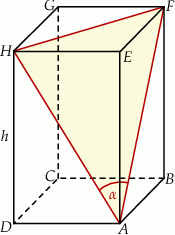
Dany jest graniastosłup prosty 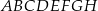 o podstawie prostokątnej
o podstawie prostokątnej 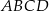 . Przekątne
. Przekątne 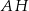 i
i 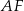 ścian bocznych tworzą kąt ostry o mierze
ścian bocznych tworzą kąt ostry o mierze  takiej, że
takiej, że 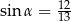 (zobacz rysunek). Pole trójkąta
(zobacz rysunek). Pole trójkąta 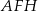 jest równe 26,4. Oblicz wysokość
jest równe 26,4. Oblicz wysokość 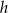 tego graniastosłupa.
tego graniastosłupa.
Punkt 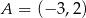 jest wierzchołkiem trójkąta równoramiennego
jest wierzchołkiem trójkąta równoramiennego 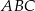 , w którym
, w którym 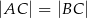 . Pole tego trójkąta jest równe 15. Bok
. Pole tego trójkąta jest równe 15. Bok 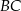 zawarty jest w prostej o równaniu
zawarty jest w prostej o równaniu 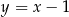 . Oblicz współrzędne wierzchołków
. Oblicz współrzędne wierzchołków 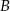 i
i 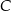 tego trójkąta.
tego trójkąta.
Rozpatrujemy wszystkie trójkąty równoramienne o obwodzie równym 18.
- Wykaż, że pole
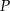 każdego z tych trójkątów, jako funkcja długości
każdego z tych trójkątów, jako funkcja długości 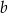 ramienia, wyraża się wzorem
ramienia, wyraża się wzorem 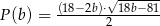 .
. - Wyznacz dziedzinę funkcji
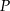 .
. - Oblicz długości boków tego z rozpatrywanych trójkątów, który ma największe pole.

