/Szkoła średnia/Zadania maturalne/Matura 2022
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis zadania.info poziom rozszerzony 26 lutego 2022 Czas pracy: 180 minut
Zadania zamknięte
Wyrażenie 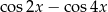 jest równe
jest równe
A) 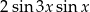 B)
B) 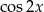 C)
C) 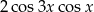 D)
D) 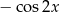
Jeżeli 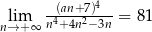 , to liczba
, to liczba  może być równa
może być równa
A) 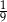 B)
B) 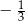 C)
C) 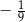 D) 3
D) 3
Wielomian 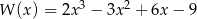 jest podzielny przez wielomian
jest podzielny przez wielomian
A) 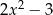 B)
B)  C)
C) 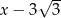 D)
D) 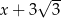
Na rysunku przedstawiono fragment wykresu pewnej funkcji 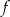 . Jeden z podanych poniżej wzorów jest wzorem tej funkcji. Wskaż wzór funkcji
. Jeden z podanych poniżej wzorów jest wzorem tej funkcji. Wskaż wzór funkcji  .
.
A) 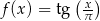 B)
B) 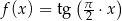
C) 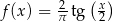 D)
D) 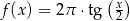
Zadania otwarte
Wyznacz punkty wspólne wykresów 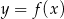 i
i 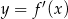 jeżeli
jeżeli 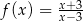 .
.
Udowodnij, że
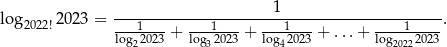
Rozwiąż nierówność
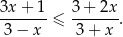
Rozwiąż równanie 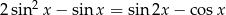 w przedziale
w przedziale 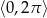 .
.
Suma trzech początkowych wyrazów nieskończonego ciągu geometrycznego 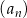 wynosi 18, a suma
wynosi 18, a suma 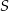 wszystkich wyrazów tego ciągu jest równa 16. Oblicz iloraz tego ciągu.
wszystkich wyrazów tego ciągu jest równa 16. Oblicz iloraz tego ciągu.
W loterii szkolnej losujemy jeden spośród 100 losów, przy czym w przypadku wyciągnięcia losu przegrywającego możemy wylosować jeszcze jeden los. Ile losów w tej loterii jest przegrywających, jeżeli prawdopodobieństwo wygranej jest równe 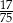 ?
?
Dla jakich wartości parametru 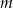 równanie
równanie 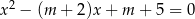 ma dwa pierwiastki różnych znaków
ma dwa pierwiastki różnych znaków 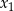 i
i 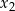 spełniające warunek
spełniające warunek 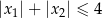 ?
?
Z wierzchołków 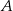 i
i 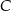 kątów ostrych równoramiennego trójkąta prostokątnego
kątów ostrych równoramiennego trójkąta prostokątnego 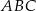 poprowadzono środkowe
poprowadzono środkowe 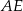 i
i 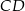 przecinające się w punkcie
przecinające się w punkcie 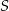 . Oblicz promień okręgu opisanego na trójkącie
. Oblicz promień okręgu opisanego na trójkącie 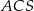 jeżeli
jeżeli 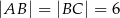 .
.
Dana jest funkcja kwadratowa 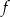 określona wzorem
określona wzorem 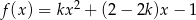 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  i
i 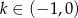 . Wyznacz równania dwóch prostopadłych stycznych do wykresu funkcji
. Wyznacz równania dwóch prostopadłych stycznych do wykresu funkcji 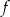 poprowadzonych w punktach, których pierwsze współrzędne różnią się o 2, jeżeli wiadomo, że funkcja
poprowadzonych w punktach, których pierwsze współrzędne różnią się o 2, jeżeli wiadomo, że funkcja 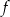 ma maksimum lokalne równe
ma maksimum lokalne równe  .
.
Punkty 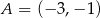 i
i 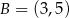 są wierzchołkami trójkąta
są wierzchołkami trójkąta 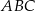 , a jego wysokości przecinają się w punkcie
, a jego wysokości przecinają się w punkcie 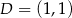 . Oblicz długość wysokości tego trójkąta opuszczonej na bok
. Oblicz długość wysokości tego trójkąta opuszczonej na bok 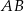 .
.
Zakład produkcyjny dostał zlecenie produkcji prostopadłościennych pudełek (całkowicie otwartych od góry) o objętości 60,75 litra. Dno pudełka ma być kwadratem i żaden z jego wymiarów nie może przekraczać 67,5 cm. Na koszt wykonania pudełka składają się – koszt wykonania 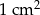 dna w wysokości 48 gorszy oraz koszt wykonania
dna w wysokości 48 gorszy oraz koszt wykonania 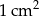 ściany bocznej w wysokości 36 groszy. Oblicz wymiary pudełka, dla których koszt jego produkcji będzie najmniejszy.
ściany bocznej w wysokości 36 groszy. Oblicz wymiary pudełka, dla których koszt jego produkcji będzie najmniejszy.

