/Szkoła średnia/Zadania maturalne/Matura 2022
Dowody w geometrii czworokąty i okręgi poziom rozszerzony
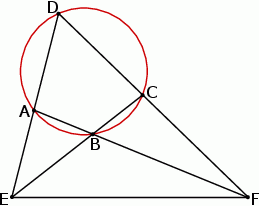
W trójkącie 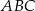 kąt wewnętrzny przy wierzchołku
kąt wewnętrzny przy wierzchołku  ma miarę
ma miarę 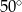 , a kąt wewnętrzny przy wierzchołku
, a kąt wewnętrzny przy wierzchołku  ma miarę
ma miarę 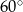 . Okrąg
. Okrąg 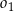 przechodzi przez punkt
przechodzi przez punkt 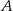 i przecina boki
i przecina boki 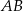 i
i 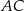 trójkąta odpowiednio w punktach
trójkąta odpowiednio w punktach 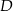 i
i 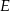 . Okrąg
. Okrąg 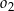 przechodzi przez punkt
przechodzi przez punkt 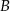 , przecina okrąg
, przecina okrąg 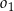 w punkcie
w punkcie 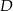 oraz w punkcie
oraz w punkcie 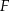 leżącym wewnątrz trójkąta
leżącym wewnątrz trójkąta 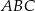 . Ponadto okrąg
. Ponadto okrąg 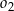 przecina bok
przecina bok 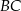 trójkąta w punkcie
trójkąta w punkcie 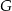 .
.
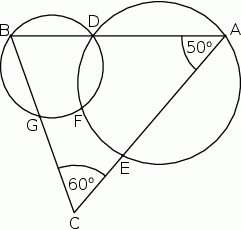
Udowodnij, że na czworokącie 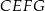 można opisać okrąg.
można opisać okrąg.
Dane są cztery okręgi. Każdy z nich jest styczny zewnętrznie do dokładnie dwóch spośród trzech pozostałych okręgów. Uzasadnij, że środki tych okręgów są wierzchołkami czworokąta, w który można wpisać okrąg.
Okrąg przechodzący przez końce przyprostokątnej 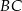 trójkąta prostokątnego
trójkąta prostokątnego 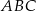 przecina drugą przyprostokątną
przecina drugą przyprostokątną 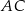 oraz przeciwprostokątną
oraz przeciwprostokątną 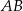 tego trójkąta odpowiednio w punktach
tego trójkąta odpowiednio w punktach 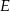 i
i 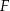 . Wykaż, że promień okręgu opisanego na trójkącie
. Wykaż, że promień okręgu opisanego na trójkącie 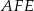 jest równy
jest równy 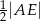 .
.
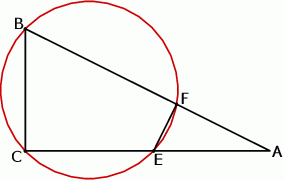
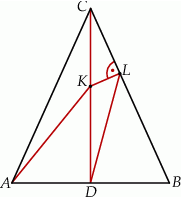
Miary kątów trójkąta 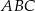 są równe
są równe 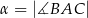 ,
, 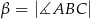 i
i 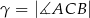 . Punkt
. Punkt 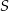 jest środkiem okręgu wpisanego w ten trójkąt, a proste zawierające odcinki
jest środkiem okręgu wpisanego w ten trójkąt, a proste zawierające odcinki 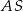 i
i 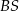 przecinają boki
przecinają boki 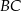 i
i 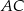 tego trójkąta w punktach odpowiednio
tego trójkąta w punktach odpowiednio 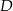 i
i 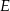 (zobacz rysunek).
(zobacz rysunek).
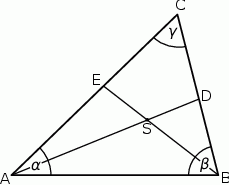
Wykaż, że jeżeli 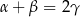 , to na czworokącie
, to na czworokącie 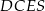 można opisać okrąg.
można opisać okrąg.
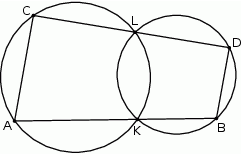
Dwa okręgi przecinają się w punktach 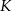 i
i 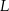 . Przez punkty
. Przez punkty 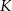 i
i 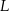 poprowadzono proste, które przecinają dane okręgi w punktach
poprowadzono proste, które przecinają dane okręgi w punktach  tak, jak pokazano to na poniższym rysunku. Wykaż, że
tak, jak pokazano to na poniższym rysunku. Wykaż, że 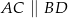 .
.
Trójkąt 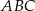 jest ostrokątny oraz
jest ostrokątny oraz 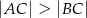 . Dwusieczna
. Dwusieczna 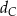 kąta
kąta 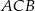 przecina bok
przecina bok 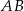 w punkcie
w punkcie 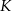 . Punkt
. Punkt 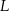 jest obrazem punktu
jest obrazem punktu 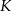 w symetrii osiowej względem dwusiecznej
w symetrii osiowej względem dwusiecznej 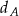 kąta
kąta 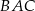 , punkt
, punkt 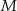 jest obrazem punktu
jest obrazem punktu 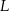 w symetrii osiowej względem dwusiecznej
w symetrii osiowej względem dwusiecznej 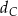 kąta
kąta 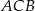 , a punkt
, a punkt 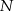 jest obrazem punktu
jest obrazem punktu 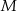 w symetrii osiowej względem dwusiecznej
w symetrii osiowej względem dwusiecznej 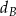 kąta
kąta  (zobacz rysunek).
(zobacz rysunek).
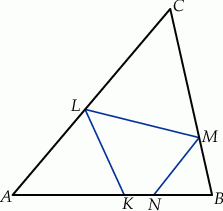
Udowodnij, że na czworokącie  można opisać okrąg.
można opisać okrąg.
Punkt 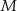 przyprostokątnej
przyprostokątnej 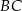 trójkąta prostokątnego
trójkąta prostokątnego 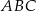 zrzutowano na przeciwprostokątną
zrzutowano na przeciwprostokątną 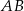 otrzymując punkt
otrzymując punkt 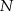 . Wykaż, że
. Wykaż, że 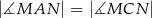 .
.
Odcinek 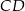 jest wysokością przedstawionego na rysunku trójkąta równoramiennego
jest wysokością przedstawionego na rysunku trójkąta równoramiennego 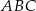 , w którym
, w którym 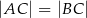 . Punkt
. Punkt 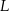 jest rzutem punktu
jest rzutem punktu  wysokości
wysokości  na bok
na bok  . Udowodnij, że
. Udowodnij, że  .
.
Wykaż, że jeżeli w czworokącie  dwusieczne kątów przy wierzchołkach
dwusieczne kątów przy wierzchołkach 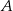 i
i 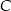 przecinają dwusieczne kątów przy wierzchołkach
przecinają dwusieczne kątów przy wierzchołkach 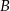 i
i 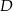 w czterech różnych punktach, to punkty te leżą na pewnym okręgu.
w czterech różnych punktach, to punkty te leżą na pewnym okręgu.
Przekątne czworokąta wypukłego 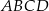 dzielą go na cztery trójkąty. Wykaż, że jeżeli promienie okręgów opisanych na tych czterech trójkątach są równe, to w czworokąt
dzielą go na cztery trójkąty. Wykaż, że jeżeli promienie okręgów opisanych na tych czterech trójkątach są równe, to w czworokąt 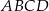 można wpisać okrąg.
można wpisać okrąg.
W czworokącie wypukłym 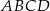 , długości boków
, długości boków 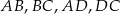 są kolejnymi wyrazami ciągu arytmetycznego. Wykaż, że dwusieczne kątów wewnętrznych tego czworokąta przecinają się w jednym punkcie.
są kolejnymi wyrazami ciągu arytmetycznego. Wykaż, że dwusieczne kątów wewnętrznych tego czworokąta przecinają się w jednym punkcie.
Przeciwległe boki czworokąta 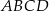 wpisanego w okrąg przecinają się w punktach
wpisanego w okrąg przecinają się w punktach 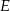 i
i 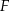 (zobacz rysunek), przy czym odcinek
(zobacz rysunek), przy czym odcinek 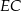 jest zawarty w dwusiecznej kąta
jest zawarty w dwusiecznej kąta 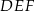 , a odcinek
, a odcinek 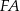 jest zawarty w dwusiecznej kąta
jest zawarty w dwusiecznej kąta 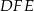 . Wykaż, że
. Wykaż, że 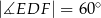 .
.
Udowodnij, że średnica okręgu wpisanego w trapez równoramienny, ma długość równą średniej geometrycznej długości podstaw trapezu.
Przez każde dwa sąsiednie wierzchołki czworokąta  wpisanego w okrąg poprowadzono okrąg (zobacz rysunek).
wpisanego w okrąg poprowadzono okrąg (zobacz rysunek).
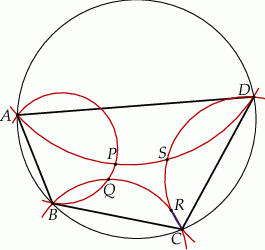
Wykaż, że punkty  , w których przecinają się te okręgi, leżą na jednym okręgu.
, w których przecinają się te okręgi, leżą na jednym okręgu.
W czworokącie wypukłym 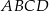 poprowadzono przekątną
poprowadzono przekątną 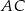 . Okręgi wpisane w trójkąty
. Okręgi wpisane w trójkąty 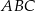 i
i 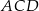 są styczne zewnętrznie. Wykaż, że w czworokąt
są styczne zewnętrznie. Wykaż, że w czworokąt 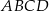 można wpisać okrąg.
można wpisać okrąg.
Trapez prostokątny 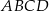 o podstawach
o podstawach 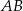 i
i 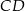 jest opisany na okręgu o promieniu
jest opisany na okręgu o promieniu  .
.
- Wykaż, że
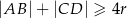 .
. - Wiedząc, że pole trapezu jest równe 4 wykaż, że
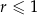 .
.
Na bokach 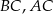 i
i 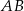 trójkąta
trójkąta 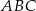 wybrano odpowiednio punkty
wybrano odpowiednio punkty 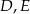 i
i 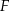 . Wykaż, że jeżeli okręgi opisane na trójkątach
. Wykaż, że jeżeli okręgi opisane na trójkątach 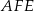 i
i 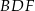 są styczne, to punkt
są styczne, to punkt 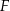 leży na okręgu opisanym na trójkącie
leży na okręgu opisanym na trójkącie 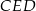 .
.

