/Szkoła średnia/Zadania maturalne/Matura 2022
Dowody w geometrii trygonometria poziom rozszerzony
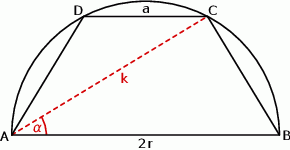
W półkole o promieniu  wpisano trapez równoramienny. Przekątna trapezu o długości
wpisano trapez równoramienny. Przekątna trapezu o długości 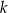 tworzy z dłuższą podstawą kąt o mierze
tworzy z dłuższą podstawą kąt o mierze  , a krótsza podstawa trapezu ma długość
, a krótsza podstawa trapezu ma długość  . Uzasadnij, że
. Uzasadnij, że 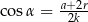 .
.
Przekątna trapezu równoramiennego tworzy z dłuższą podstawą kąt 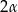 , a z ramieniem kąt
, a z ramieniem kąt  . Wykaż, że stosunek pól trójkątów, na które został podzielony trapez tą przekątną, jest równy
. Wykaż, że stosunek pól trójkątów, na które został podzielony trapez tą przekątną, jest równy 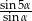 .
.
Wykaż, że jeśli 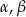 są kątami ostrymi trójkąta prostokątnego, to
są kątami ostrymi trójkąta prostokątnego, to 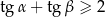 .
.
Pole trapezu równoramiennego opisanego na okręgu jest równe 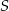 , a kąt ostry przy podstawie ma miarę
, a kąt ostry przy podstawie ma miarę  . Wykaż, że ramię tego trapezu ma długość
. Wykaż, że ramię tego trapezu ma długość 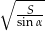 .
.
Wykaż, że jeżeli kąty 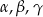 trójkąta
trójkąta 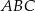 spełniają warunek
spełniają warunek 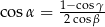 to trójkąt jest równoramienny.
to trójkąt jest równoramienny.
W trójkącie ostrokątnym 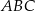 bok
bok 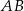 ma długość
ma długość  , długość boku
, długość boku 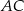 jest równa
jest równa 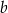 oraz
oraz 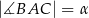 . Dwusieczna kąta
. Dwusieczna kąta 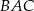 przecina bok
przecina bok 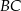 trójkąta w punkcie
trójkąta w punkcie 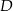 i odcinek
i odcinek 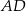 ma długość
ma długość 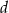 . Wykaż, że
. Wykaż, że
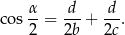
Wykaż, że jeżeli w trójkącie 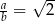 to
to 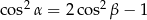 .
.
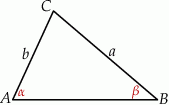
W trójkącie prostokątnym 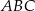 przyprostokątne mają długości
przyprostokątne mają długości 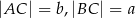 , a wysokość opuszczona z wierzchołka kąta prostego ma długość
, a wysokość opuszczona z wierzchołka kąta prostego ma długość 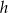 .
.
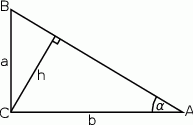
Wykaż, że jeżeli 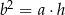 to
to 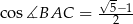 .
.
Wykaż, że jeżeli  i
i 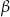 są kątami trójkąta oraz
są kątami trójkąta oraz 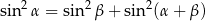 to trójkąt ten jest prostokątny.
to trójkąt ten jest prostokątny.
W trójkącie 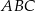 środkowa
środkowa 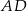 jest prostopadła do boku
jest prostopadła do boku 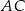 . Kąt
. Kąt 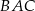 ma miarę
ma miarę 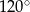 . Wykaż, że
. Wykaż, że 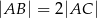 .
.
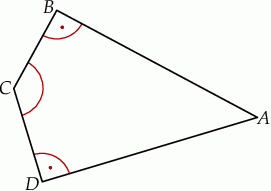
W czworokącie wypukłym  (zobacz rysunek poniżej) dane są kąty:
(zobacz rysunek poniżej) dane są kąty: 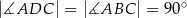 oraz
oraz 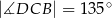 . Wykaż, że
. Wykaż, że 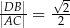 .
.
Kąty w trójkącie mają miary: 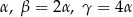 . Wykaż, że długości boków
. Wykaż, że długości boków 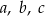 tego trójkąta spełniają równość:
tego trójkąta spełniają równość: 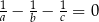 .
.
Wykaż, że jeżeli promień okręgu opisanego na trójkącie równoramiennym jest dwa razy dłuższy od promienia okręgu wpisanego w ten trójkąt, to trójkąt ten jest równoboczny.

