/Szkoła średnia/Zadania maturalne/Matura 2022
Dowody w geometrii podobieństwo I
Dany jest trapez 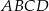 o podstawach
o podstawach 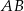 i
i 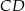 . Przekątne tego trapezu przecinają się w punkcie
. Przekątne tego trapezu przecinają się w punkcie 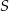 . Wykaż, że
. Wykaż, że 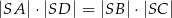 .
.
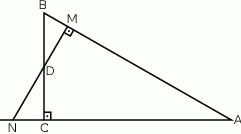
Przez środek 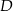 przyprostokątnej
przyprostokątnej 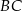 trójkąta prostokątnego
trójkąta prostokątnego 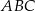 poprowadzono prostą prostopadłą do przeciwprostokątnej
poprowadzono prostą prostopadłą do przeciwprostokątnej 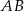 . Prosta ta przecina proste
. Prosta ta przecina proste 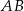 i
i 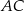 odpowiednio w punktach
odpowiednio w punktach 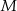 i
i 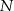 . Wykaż, że
. Wykaż, że 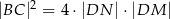 .
.
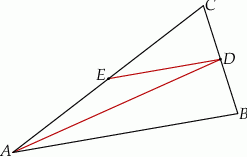
W trapezie 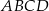 punkt
punkt 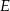 jest środkiem ramienia
jest środkiem ramienia 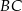 . Z wierzchołka
. Z wierzchołka 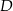 poprowadzono prostą przecinającą ramię
poprowadzono prostą przecinającą ramię 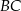 w punkcie
w punkcie 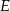 . Proste
. Proste 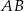 i
i 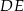 przecinają się w punkcie
przecinają się w punkcie 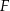 (zobacz rysunek). Wykaż, że
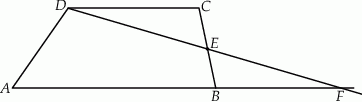
(zobacz rysunek). Wykaż, że 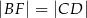 .
.
Uzasadnij, że jeżeli 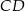 jest wysokością trójkąta prostokątnego
jest wysokością trójkąta prostokątnego 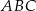 , w którym
, w którym 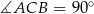 to
to 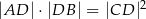 .
.
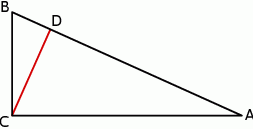
Punkty 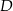 i
i 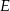 są środkami boków
są środkami boków 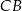 i
i 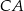 trójkąta
trójkąta 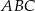 (zobacz rysunek). Wykaż, że odległość punktu
(zobacz rysunek). Wykaż, że odległość punktu 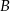 od prostej
od prostej 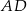 jest dwa razy większa od odległości punktu
jest dwa razy większa od odległości punktu 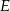 od prostej
od prostej 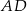 .
.
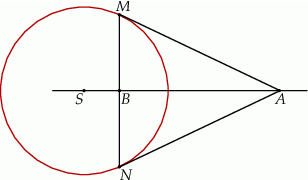
Na okręgu o promieniu  wybrano punkty
wybrano punkty  i
i  w ten sposób, że proste
w ten sposób, że proste 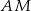 i
i 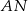 są styczne do okręgu. Punkt
są styczne do okręgu. Punkt 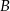 jest punktem wspólnym odcinka
jest punktem wspólnym odcinka 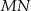 i prostej łączącej
i prostej łączącej 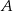 ze środkiem
ze środkiem 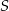 tego okręgu. Wykaż, że
tego okręgu. Wykaż, że 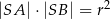 .
.
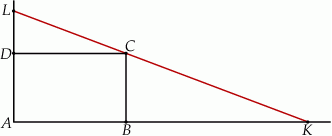
Przez wierzchołek 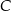 prostokąta
prostokąta 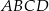 poprowadzono prostą, która przecięła proste
poprowadzono prostą, która przecięła proste 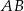 i
i 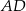 w punktach
w punktach 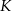 i
i 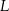 odpowiednio. Wykaż, że
odpowiednio. Wykaż, że 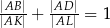 .
.
W trójkącie 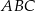 wysokość
wysokość 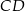 dzieli bok
dzieli bok 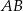 na odcinki
na odcinki 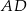 i
i 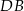 (rysunek), przy czym
(rysunek), przy czym 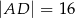 i
i 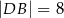 . Wykaż, że symetralna boku
. Wykaż, że symetralna boku 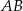 dzieli bok
dzieli bok 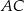 w stosunku 3:1.
w stosunku 3:1.
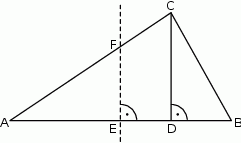
Trójkąt 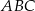 jest prostokątny. Punkt
jest prostokątny. Punkt 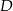 jest spodkiem wysokości opuszczonej na przeciwprostokątną
jest spodkiem wysokości opuszczonej na przeciwprostokątną 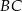 oraz
oraz 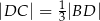 (patrz rysunek). Wykaż, że
(patrz rysunek). Wykaż, że 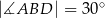 .
.
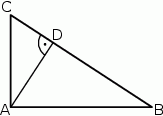
Przekątne czworokąta 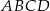 wpisanego w okrąg przecinają się w punkcie
wpisanego w okrąg przecinają się w punkcie 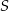 , a punkt
, a punkt 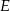 jest takim punktem przekątnej
jest takim punktem przekątnej 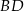 , że
, że 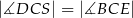 (zobacz rysunek).
(zobacz rysunek).
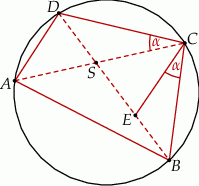
Wykaż, że 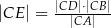 .
.
Pole kwadratu 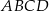 jest równe 16. Punkt
jest równe 16. Punkt 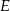 jest środkiem boku
jest środkiem boku 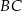 , a punkt
, a punkt 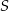 punktem przecięcia przekątnej
punktem przecięcia przekątnej 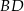 kwadratu i odcinka
kwadratu i odcinka 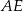 . Wykaż, że odległość punktu
. Wykaż, że odległość punktu 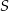 od boku
od boku 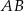 jest równa
jest równa 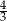 .
.
Punkt 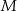 jest punktem wspólnym przekątnych trapezu prostokątnego
jest punktem wspólnym przekątnych trapezu prostokątnego 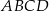 . Punkt
. Punkt 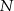 jest punktem wspólnym przekątnej
jest punktem wspólnym przekątnej 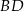 i wysokości
i wysokości 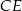 opuszczonej na dłuższą podstawę
opuszczonej na dłuższą podstawę 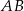 . Wykaż, że
. Wykaż, że 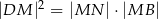 .
.
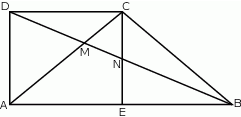
Trójkąt 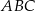 jest równoboczny. Punkt
jest równoboczny. Punkt 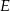 leży na wysokości
leży na wysokości 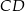 tego trójkąta oraz
tego trójkąta oraz 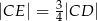 . Punkt
. Punkt 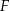 leży na boku
leży na boku 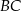 i odcinek
i odcinek 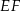 jest prostopadły do
jest prostopadły do 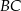 (zobacz rysunek).
(zobacz rysunek).
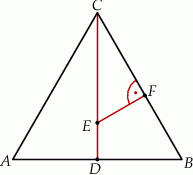
Wykaż, że 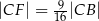 .
.
W trapez 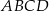 wpisano okrąg o środku
wpisano okrąg o środku 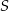 . Okrąg ten jest styczny do ramion
. Okrąg ten jest styczny do ramion 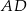 i
i 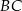 tego trapezu w punktach odpowiednio
tego trapezu w punktach odpowiednio 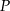 i
i 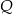 (zobacz rysunek).
(zobacz rysunek).
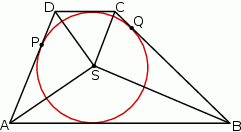
Uzasadnij, że trójkąt 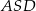 jest prostokątny. Wykaż, że
jest prostokątny. Wykaż, że 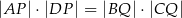 .
.
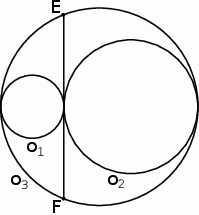
Dane są trzy okręgi 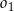 ,
, 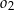 i
i 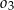 . Okręgi
. Okręgi 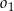 ,
, 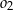 są styczne zewnętrznie, jednocześnie są styczne wewnętrznie do okręgu
są styczne zewnętrznie, jednocześnie są styczne wewnętrznie do okręgu 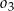 (patrz rysunek). Promienie okręgów
(patrz rysunek). Promienie okręgów 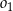 i
i 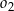 są odpowiednio równe
są odpowiednio równe 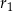 i
i 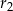 , a środki wszystkich trzech okręgów leżą na jednej prostej. Uzasadnij, że długość odcinka
, a środki wszystkich trzech okręgów leżą na jednej prostej. Uzasadnij, że długość odcinka 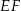 jest równa
jest równa 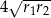 , gdzie odcinek
, gdzie odcinek 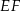 jest cięciwą okręgu
jest cięciwą okręgu 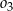 i zawiera się we wspólnej stycznej okręgów
i zawiera się we wspólnej stycznej okręgów 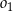 i
i 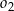 .
.
Dany jest trójkąt równoramienny 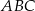 , w którym
, w którym 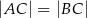 . Na ramieniu
. Na ramieniu 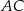 tego trójkąta wybrano punkt
tego trójkąta wybrano punkt 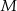 (
(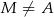 i
i 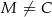 ), a na ramieniu
), a na ramieniu 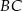 wybrano punkt
wybrano punkt 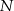 , w taki sposób, że
, w taki sposób, że 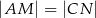 . Przez punkty
. Przez punkty 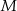 i
i 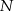 poprowadzono proste prostopadłe do podstawy
poprowadzono proste prostopadłe do podstawy 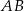 tego trójkąta, które wyznaczają na niej punkty
tego trójkąta, które wyznaczają na niej punkty 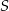 i
i 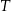 . Udowodnij, że
. Udowodnij, że 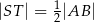 .
.

