/Szkoła średnia/Funkcje - wykresy/Wartość bezwzględna

Zadanie nr 2728985

Dodaj do ulubionych
Dodaj do rozwiązanych

Dana jest funkcja kwadratowa 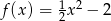1 2 f(x) = 2 x − 2 .

  • Narysuj wykres funkcji 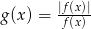|f(x)| g(x) = f(x)- , której dziedziną jest zbiór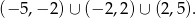
    (− 5,− 2) ∪ (− 2,2)∪ (2,5).
  • Zapisz zbiór rozwiązań nierówności g(x ) < 0 .

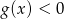Rozwiązanie

  • Na mocy definicji wartości bezwzględnej mamy
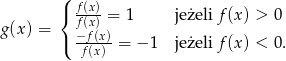
    ( { f(x)= 1 jeżeli f(x) > 0 g(x) = f(x) ( −ff((xx)) = − 1 jeżeli f(x) < 0.

    Pozostało zatem ustalić kiedy 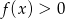f(x) > 0 . Wykres funkcji 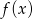f(x) to parabola o ramionach skierowanych w górę i miejscach zerowych -2 i 2 (lewy wykres na obrazku).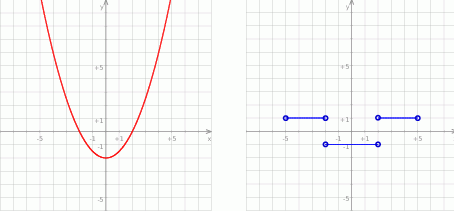

    PIC

    Zatem

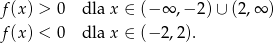
    f(x) > 0 dla x ∈ (− ∞ ,− 2)∪ (2,∞ ) f(x) < 0 dla x ∈ (− 2,2).

    Mamy stąd

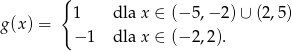
    { 1 dla x ∈ (− 5,− 2)∪ (2,5) g (x) = − 1 dla x ∈ (− 2,2).

    Teraz bez problemu szkicujemy wykres funkcji 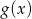g (x) – prawy wykres na obrazku.

  • Z poprzedniego podpunktu mamy 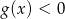g(x) < 0 jeżeli x ∈ (− 2,2 ) .  
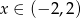    Odpowiedź: x ∈ (− 2,2)
Wersja PDF