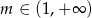/Szkoła średnia/Funkcje - wykresy/Wartość bezwzględna

Zadanie nr 3798362

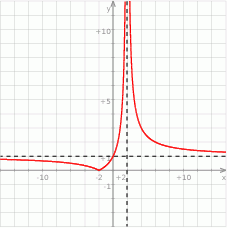
Na rysunku przedstawiony jest fragment wykresu funkcji określonej wzorem 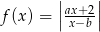| | f (x) = ||ax+2|| x−b .

PIC

  • Oblicz a i b .
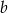  • Narysuj wykres funkcji określonej wzorem y = f (|x |) .
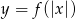  • Podaj wszystkie wartości parametru 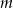m , dla których równanie 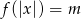f(|x|) = m ma cztery rozwiązania.
Wersja PDF

Rozwiązanie

  • Z wykresu wiać, że do dziedziny funkcji nie należy liczba 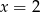x = 2 , więc 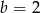b = 2 . Zapiszmy wzór funkcji homograficznej pod wartością bezwzględną w postaci kanonicznej.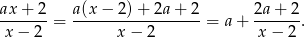
    ax + 2 a(x − 2)+ 2a + 2 2a+ 2 -------= ------------------= a + ------. x − 2 x− 2 x − 2

    Z wykresu widać, że funkcja homograficzna 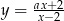y = axx+−22 nie przyjmuje wartości 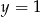y = 1 , więc musi być 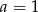a = 1 i funkcja 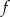f określona jest wzorem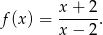

    x+ 2 f(x) = -----. x− 2

     
    Odpowiedź: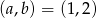 (a,b) = (1,2)

  • Wykres funkcji 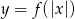y = f(|x|) powstaje z wykresu funkcji 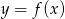y = f(x) przez odbicie części wykresu znajdującego się na prawo od osi Oy względem osi Oy . Resztę wykresu usuwamy.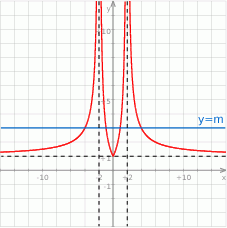
    PIC
  • Odczytujemy ze zrobionego przed chwilą wykresu.  
    Odpowiedź: m ∈ (1,+ ∞ )
Wersja PDF