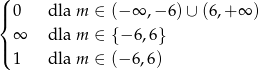/Szkoła średnia/Funkcje - wykresy/Wartość bezwzględna

Zadanie nr 4062714

Dodaj do ulubionych
Dodaj do rozwiązanych

Naszkicuj wykres funkcji 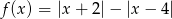f (x) = |x+ 2|− |x − 4| , na podstawie wykresu określ liczbę rozwiązań równania 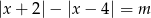|x + 2|− |x − 4| = m w zależności od parametru m .

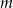Rozwiązanie

Zapiszmy wzór funkcji 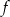f bez wartości bezwzględnej.

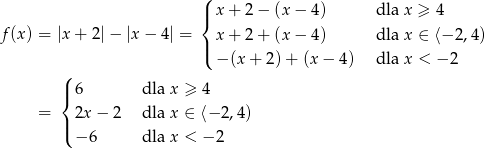
( |{ x + 2 − (x − 4) dla x ≥ 4 f(x) = |x + 2|− |x− 4| = x + 2 + (x − 4) dla x ∈ ⟨− 2,4) |( ( − (x + 2) + (x − 4) dla x < − 2 | 6 dla x ≥ 4 { = | 2x − 2 dla x ∈ ⟨− 2,4) ( − 6 dla x < − 2

Szkicujemy teraz wykres funkcji f .

PIC

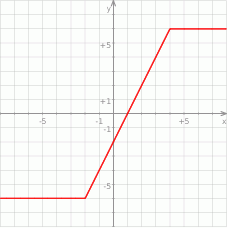
Z wykresu odczytujemy liczbę rozwiązań równania 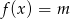f(x ) = m (czyli liczbę punktów wspólnych wykresu funkcji 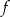f z prostą y = m ).

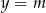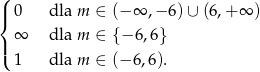
( |{ 0 dla m ∈ (−∞ ,− 6) ∪ (6,+ ∞ ) |( ∞ dla m ∈ {− 6,6} 1 dla m ∈ (−6 ,6).

 
Odpowiedź: ( | 0 dla m ∈ (− ∞ ,− 6)∪ (6,+ ∞ ) { | ∞ dla m ∈ {− 6,6} ( 1 dla m ∈ (− 6,6)

Wersja PDF