/Szkoła średnia/Funkcje - wykresy/Wartość bezwzględna

Zadanie nr 4574162

Dodaj do ulubionych
Dodaj do rozwiązanych

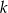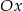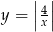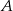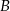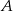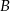Prosta k równoległa do osi Ox przecina wykres funkcji ||4|| y = |x| w dwóch punktach A i B . Wyznacz współrzędne punktów A i B jeżeli wiadomo, że razem z punktem 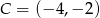C = (− 4,− 2) tworzą trójkąt o polu 6.

Rozwiązanie

Rozpoczynamy od rysunku – wykres 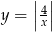||4|| y = |x| powstaje z wykresu 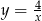4 y = x przez odbicie części poniżej osi 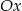Ox do góry.

PIC

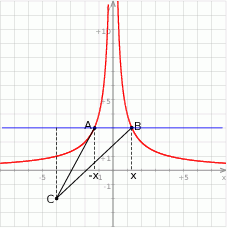
Funkcja 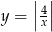|| || y = | 4x| jest parzysta, więc pozioma prosta przecina jej wykres w punktach położonych symetrycznie względem osi 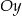Oy . Możemy więc oznaczyć współrzędne tych punktów przez

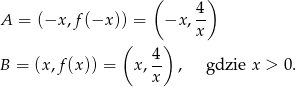
( 4) A = (−x ,f(−x )) = −x , -- ( ) x -4 B = (x ,f(x)) = x,x , gdzie x > 0.

Sposób I

Podstawa trójkąta 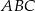ABC ma więc długość 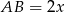AB = 2x , a wysokość 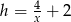h = x4+ 2 . Podane pole trójkąta 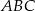ABC prowadzi do równania

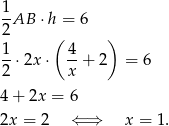
1- 2AB ⋅h = 6 1 ( 4 ) -⋅ 2x⋅ --+ 2 = 6 2 x 4 + 2x = 6 2x = 2 ⇐ ⇒ x = 1.

Zatem 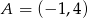A = (− 1,4) i B = (1,4) .

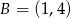Sposób II

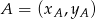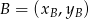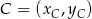Korzystamy ze wzoru na pole trójkąta o wierzchołkach A = (xA,yA ) , B = (xB,yB ) i C = (xC ,yC) .

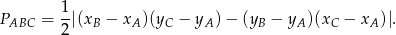
1 PABC = --|(xB − xA)(yC − yA) − (yB − yA )(xC − xA )|. 2

W naszej sytuacji otrzymujemy równanie

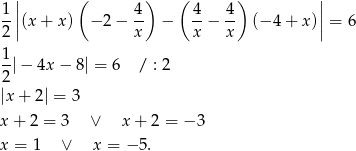
| | 1 | ( 4) ( 4 4) | --||(x + x ) − 2− -- − --− -- (− 4 + x)|| = 6 2 x x x 1- 2|− 4x − 8| = 6 / : 2 |x + 2 | = 3 x+ 2 = 3 ∨ x + 2 = − 3 x = 1 ∨ x = − 5.

Przy naszych oznaczeniach 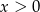x > 0 , czyli 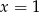x = 1 . Zatem 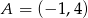A = (− 1,4 ) i B = (1,4) .  
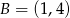Odpowiedź: 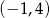(− 1,4) i (1,4)

Wersja PDF