/Szkoła średnia/Funkcje - wykresy/Wartość bezwzględna

Zadanie nr 4922457

Dodaj do ulubionych
Dodaj do rozwiązanych

Dana jest funkcja 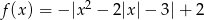2 f(x ) = − |x − 2 |x |− 3|+ 2 ; x ∈ R .

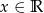  • Narysuj wykres tej funkcji, stosując odpowiednie przekształcenia, wymień je.
  • Na podstawie wykresu funkcji 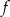f określ zbiór wartości tej funkcji.
  • Podaj liczbę miejsc zerowych funkcji f .
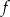  • Podaj współrzędne punktu przecięcia wykresu z osią OY .
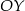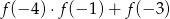  • Podaj znak liczby f(− 4 )⋅f(− 1) + f(− 3 ) .
  • Czy funkcja jest rożnowartościowa? Czy jest parzysta lub nieparzysta?

Rozwiązanie

  • Jeżeli zpiszemy wzór funkcji w postaci
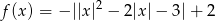
    f(x) = − ||x|2 − 2|x|− 3 |+ 2

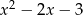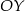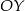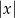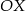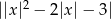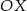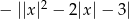    to widać jak należy narysować jej wykres: rysujemy parabolę: x2 − 2x − 3 , zostawiamy jej część na prawo od osi OY i kopiujemy tę część, odbijając względem osi OY (to przekształcenie odpowiada zamianie x na |x | ). Potem odbijamy część wykresu poniżej osi OX do góry (mamy teraz wykres 2 ||x| − 2 |x |− 3| ). Odbijamy całość względem osi OX (mamy 2 − ||x| − 2|x| − 3| ) i przesuwamy wszystko o dwie jednostki do góry.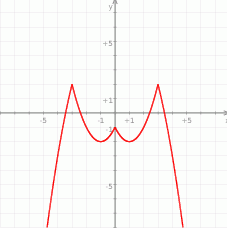

    PIC
  • Z wykresu widzimy, że zbiór wartości to przedział (− ∞ ,2⟩ .  
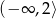    Odpowiedź: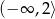 (− ∞ ,2⟩
  • Są 4 miejsca zerowe.  
    Odpowiedź: 4
  • Odczytujemy z wykresu: (0,− 1) .  
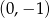    Odpowiedź: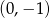 (0,− 1)
  • Liczymy
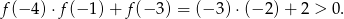
    f(− 4) ⋅f(− 1) + f(− 3) = (−3 )⋅(− 2) + 2 > 0.

     
    Odpowiedź: Dodatni

  • Widać z wykresu, że funkcja nie jest różnowartościowa i jest parzysta.  
    Odpowiedź: Nie jest różnowartościowa. Jest parzysta
Wersja PDF