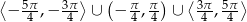/Szkoła średnia/Funkcje - wykresy/Wartość bezwzględna

Zadanie nr 7838289

Dodaj do ulubionych
Dodaj do rozwiązanych

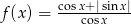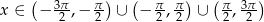Narysuj wykres funkcji cosx+|sin-x| f (x) = cosx dla ( 3π- π) ( π- π) (π- 3π) x ∈ − 2 ,− 2 ∪ − 2, 2 ∪ 2 ,2 . Podaj zbiór rozwiązań nierówności 0 ≤ f(x) < 2 .

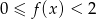Rozwiązanie

Zauważmy, że

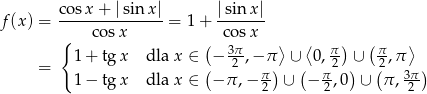
co sx + |sinx | |sinx | f (x) = ---------------= 1+ ------- { cos x ( cosx ⟩ ⟨ ) ( ⟩ 1 + tg x dla x ∈ − 3π-,− π ∪ 0, π ∪ π,π = ( 2 π) ( π-2 ) 2( 3π-) 1 − tg x dla x ∈ − π ,− 2 ∪ − 2,0 ∪ π, 2

Teraz bez trudu szkicujemy wykres

PIC

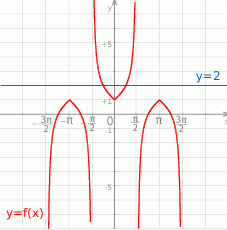
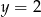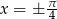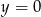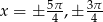Zauważmy, że prosta y = 2 przecina wykres funkcji dla x = ± π4- , a prostą y = 0 dla x = ± 5π,± 3π- 4 4 . Zatem rozwiązaniem nierówności 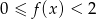0 ≤ f (x ) < 2 jest zbiór

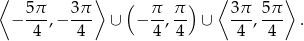
⟨ ⟩ ⟨ ⟩ 5π 3π ( π π ) 3π 5π − ---,− --- ∪ − --,-- ∪ ---,--- . 4 4 4 4 4 4

 
Odpowiedź: ⟨ 5π 3π⟩ ( π π ) ⟨ 3π 5π⟩ − 4-,− -4- ∪ − -4,4- ∪ 4-,-4-

Wersja PDF