/Szkoła średnia/Funkcje - wykresy/Wartość bezwzględna

Zadanie nr 8628501

Dodaj do ulubionych
Dodaj do rozwiązanych

Napisz wzór i naszkicuj wykres funkcji 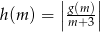||g(m-)|| h (m) = |m+ 3| wiedząc, że funkcja 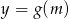y = g(m ) każdej liczbie rzeczywistej 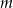m przyporządkowuje najmniejszą wartość funkcji kwadratowej 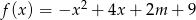f(x) = −x 2 + 4x + 2m + 9 w przedziale ⟨− 1,3⟩ .

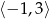Rozwiązanie

Ustalmy najpierw jaki jest wzór funkcji 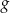g . Zauważmy, że wykresem funkcji 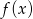f (x) jest parabola o ramionach skierowanych w dół, której wierzchołek ma pierwszą współrzędną równą

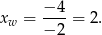
x = −-4-= 2. w − 2

Ponieważ liczba ta znajduje się bliżej prawego końca przedziału 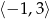⟨− 1,3⟩ , to najmniejszą wartością funkcji 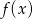f(x) na tym przedziale będzie

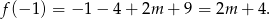
f(− 1) = − 1 − 4+ 2m + 9 = 2m + 4.

W takim razie

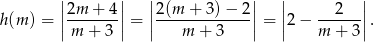
| | | | | | |2m-+-4-| |2(m-+--3)−-2-| | --2---| h (m) = ||m + 3 || = || m + 3 || = ||2− m + 3 ||.

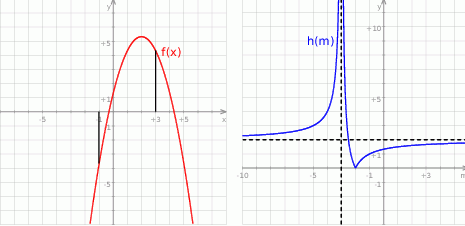
Aby naszkicować teraz wykres funkcji 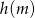h (m) , rysujemy najpierw hiperbolę 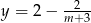-2-- y = 2− m+ 3 (jest to hiperbola 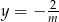-2 y = − m przesunięta o 3 jednostki w lewo i 2 do góry). Następnie odbijamy część wykresu znajdującą się poniżej osi 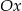Ox do góry.

PIC

Wersja PDF