/Szkoła średnia/Funkcje - wykresy/Wartość bezwzględna

Zadanie nr 9120171

Dodaj do ulubionych
Dodaj do rozwiązanych

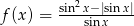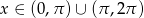Dana jest funkcja f określona wzorem sin2x−|sinx|- f(x) = sin x dla x ∈ (0,π) ∪ (π ,2 π) .

  • Naszkicuj wykres funkcji f .
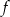  • Wyznacz miejsca zerowe funkcji f .

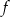Rozwiązanie

  • Rozpiszmy wzór funkcji 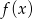f (x) , korzystając z definicji wartości bezwzględnej.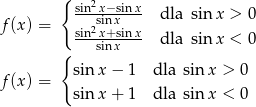
    { sin2x−-sinx- dla sinx > 0 f(x ) = sin2sxin+-xsinx- sin x dla sinx < 0 { f(x ) = sinx − 1 dla sinx > 0 sinx + 1 dla sinx < 0

    Uwzględniając podaną dziedzinę funkcji otrzymujemy:

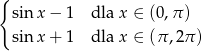
    { sin x − 1 dla x ∈ (0,π ) sin x + 1 dla x ∈ (π ,2π )

    Możemy zatem naszkicować wykres funkcji.

    PIC
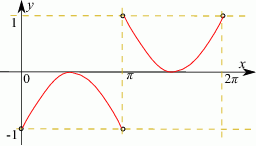
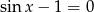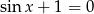  • Aby wyznaczyć miejsca zerowe musimy rozwiązać równania sin x− 1 = 0 oraz sin x+ 1 = 0 w odpowiednich przedziałach. Jedyne rozwiązania tych równań to 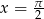π- x = 2 oraz 3π- x = 2 .  
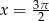    Odpowiedź: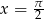 x = π2 lub x = 3π2-
Wersja PDF