/Szkoła średnia/Funkcje - wykresy/Wartość bezwzględna

Zadanie nr 9512834

Dodaj do ulubionych
Dodaj do rozwiązanych

Naszkicuj wykres funkcji 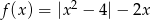2 f (x) = |x − 4|− 2x . Określ liczbę rozwiązań równania 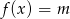f (x) = m w zależności od wartości parametru m .

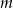Rozwiązanie

Żeby opuścić wartość bezwzględną musimy wiedzieć jaki jest znak wyrażenia 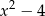x 2 − 4 . Ponieważ 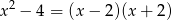x2 − 4 = (x− 2)(x+ 2) , mamy

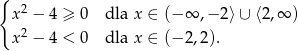
{ x 2 − 4 ≥ 0 dla x ∈ (− ∞ ,− 2⟩∪ ⟨2,∞ ) x 2 − 4 < 0 dla x ∈ (− 2,2).

Zatem

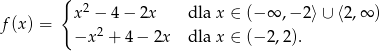
{ 2 f(x) = x − 4− 2x dla x ∈ (− ∞ ,− 2⟩ ∪ ⟨2,∞ ) −x 2 + 4− 2x dla x ∈ (− 2,2).

Musimy teraz narysować obie te parabole na odpowiednich przedziałach. Pierwsza z nich ma wierzchołek w punkcie

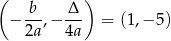
( b Δ ) − --,− --- = (1,− 5) 2a 4a

i przechodzi przez punkty 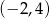(− 2,4) , (4 ,4) .

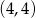Druga ma wierzchołek w punkcie 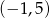(− 1,5 ) i przechodzi przez punkty 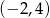(− 2,4) i (2,− 4) .

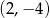Możemy teraz narysować żądany wykres.

PIC

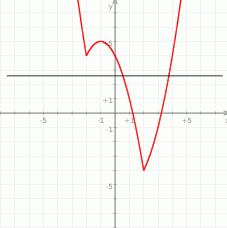
Bez trudu odczytujemy z niego ilość rozwiązań równania 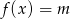f (x) = m .

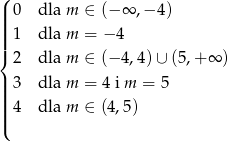
( ||| 0 dla m ∈ (− ∞ ,− 4) ||| 1 dla m = −4 ||{ 2 dla m ∈ (− 4,4) ∪ (5,+ ∞ ) || 3 dla m = 4 i m = 5 ||| |||( 4 dla m ∈ (4,5)

 
Odpowiedź: ( 0 dla m ∈ (−∞ ,− 4) |||| ||| 1 dla m = − 4 |{ 2 dla m ∈ (−4 ,4)∪ (5,+ ∞ ) ||| 3 dla m = 4 i m = 5 ||| 4 dla m ∈ (4,5) ||(

Wersja PDF