Zadanie nr 9527003
Proste 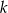 i
i 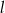 są równoległe do osi
są równoległe do osi 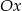 i przecinają wykres funkcji
i przecinają wykres funkcji 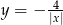 odpowiednio w punktach
odpowiednio w punktach 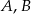 i
i 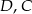 w ten sposób, że czworokąt
w ten sposób, że czworokąt 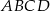 jest trapezem o polu 6 i wysokości 2. Oblicz obwód trapezu
jest trapezem o polu 6 i wysokości 2. Oblicz obwód trapezu 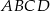 .
.
Rozwiązanie
Wykres funkcji 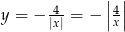 powstaje z wykresu funkcji
powstaje z wykresu funkcji 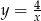 przez odbicie części powyżej osi
przez odbicie części powyżej osi 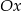 na dół.
na dół.
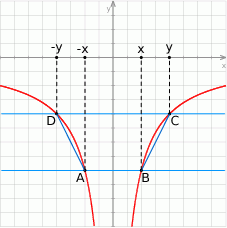
Ponieważ funkcja ta jest parzysta, proste 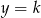 i
i 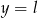 przecinają jej wykres w punktach położonych symetrycznie względem osi
przecinają jej wykres w punktach położonych symetrycznie względem osi 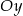 . Możemy więc oznaczyć współrzędne tych punktów przez
. Możemy więc oznaczyć współrzędne tych punktów przez
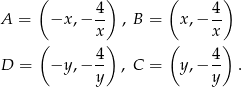
Załóżmy ponadto, że jest tak jak na obrazku, czyli 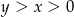 . Podstawy trapezu mają długości
. Podstawy trapezu mają długości 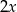 i
i 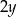 , więc podane pole daje równanie
, więc podane pole daje równanie
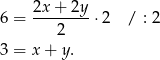
Wysokość trapezu jest równa
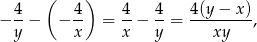
skąd mamy drugie równanie
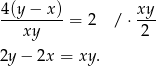
Podstawiamy teraz w tym równaniu 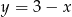 .
.
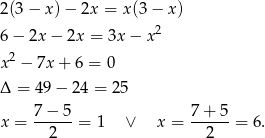
Mamy wtedy 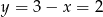 i
i 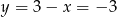 odpowiednio. Drugie rozwiązanie jest sprzeczne z naszym założeniem
odpowiednio. Drugie rozwiązanie jest sprzeczne z naszym założeniem 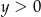 , więc musi być
, więc musi być 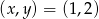 . Wtedy
. Wtedy
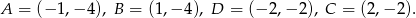
Podstawy trapezu mają długości 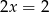 i
i 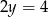 , a ramię ma długość
, a ramię ma długość
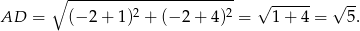
Obwód trapezu jest więc równy
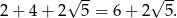
Odpowiedź: