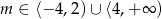/Szkoła średnia/Funkcje - wykresy/Wartość bezwzględna

Zadanie nr 9776938

Dodaj do ulubionych
Dodaj do rozwiązanych

Narysuj wykres funkcji 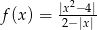|x2−4| f (x) = 2−|x| , a następnie określ, dla jakich wartości parametru 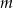m równanie 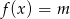f(x ) = m nie ma rozwiązania.

Rozwiązanie

Sposób I

Zauważmy, że funkcja 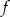f jest parzysta (tzn. 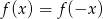f(x) = f (−x ) ), więc wystarczy narysować jej wykres dla 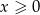x ≥ 0 , a potem skopiować otrzymany wykres przez odbicie względem osi Oy .

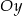Jeżeli 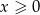x ≥ 0 to

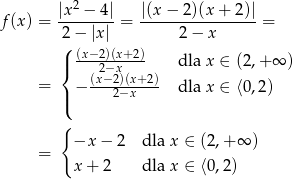
|x 2 − 4 | |(x− 2)(x+ 2)| f(x) = 2-−-|x|-= -----2-−-x------ = ( |{ (x−2)(x+2) dla x ∈ (2,+ ∞ ) (2x−−x2)(x+-2) = | − 2−x dla x ∈ ⟨0,2) ( { −x − 2 dla x ∈ (2,+ ∞ ) = x+ 2 dla x ∈ ⟨0,2)

Teraz bez trudu szkicujemy wykres.

PIC

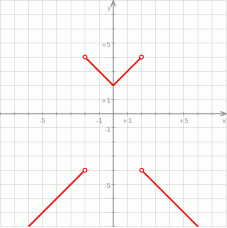
Za wykresu widzimy, że równanie 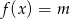f (x) = m nie ma rozwiązań dla

m ∈ ⟨− 4,2) ∪ ⟨4,+ ∞ ).

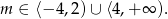
Sposób II

Daną funkcję możemy zapisać w postaci

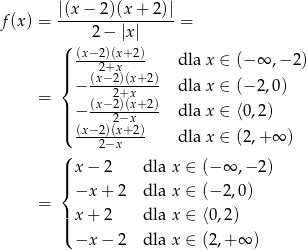
f(x) = |(x-−--2)(x+--2)|= 2 − |x| (| (x−2)(x+2) ||| 2+x dla x ∈ (− ∞ ,− 2) { − (x−22)+(xx+2) dla x ∈ (− 2,0) = | (x−2)(x+2) ||| − 2−x dla x ∈ ⟨0,2) ( (x−2)(x+2) dla x ∈ (2,+ ∞ ) ( 2−x || x − 2 dla x ∈ (− ∞ ,− 2) |{ −x + 2 dla x ∈ (− 2,0) = ||| x + 2 dla x ∈ ⟨0,2 ) ( −x − 2 dla x ∈ (2,+ ∞ )

Dalej postępujemy tak samo jak w pierwszym sposobie.  
Odpowiedź: m ∈ ⟨− 4,2) ∪ ⟨4,+ ∞ )

Wersja PDF