/Szkoła podstawowa/Egzamin ósmoklasisty/Egzamin 2022
Próbny Egzamin Ósmoklasisty
z Matematyki Zestaw przygotowany przez serwis zadania.info 23 kwietnia 2022 Czas pracy: 100 minut
Na diagramie słupkowym przedstawiono liczby medali zdobytych na czterech letnich igrzyskach olimpijskich przez reprezentację Polski.
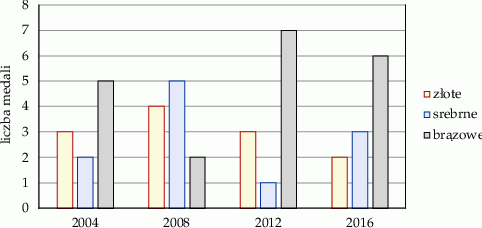
Oceń prawdziwość podanych zdań, dotyczących medali zdobytych przez reprezentację Polski podczas letnich igrzysk olimpijskich w latach 2004–2016. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Na igrzyskach zdobyto więcej medali złotych niż srebrnych. | P | F |
| Podczas letnich igrzysk olimpijskich średnio zdobywano 3 srebrne medale. | P | F |
Batony czekoladowe zapakowano do 492 jednakowych pudełek. Do każdego z tych pudełek włożono po 12 batonów. Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Liczba wszystkich spakowanych batonów jest podzielna przez 48. | P | F |
| Wszystkie te batony można byłoby spakować do większych pudełek – po 32 batony w każdym. | P | F |
Uzupełnij zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
Wartość wyrażenia 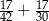 jest liczbą A/B .
jest liczbą A/B .
A) mniejszą od 1 B) większą od 1
Wartość wyrażenia 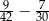 jest liczbą C/D .
jest liczbą C/D .
C) ujemną D) dodatnią
Ile spośród liczb: 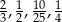 spełnia warunek
spełnia warunek 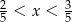 ?
?
Wybierz odpowiedź spośród podanych.
A) Jedna liczba. B) Dwie liczby. C) Trzy liczby. D) Cztery liczby.
Podatek od dochodów za rok 2016 w Polsce był obliczany według sposobów przedstawionych w poniższej tabeli.
| Podstawa obliczenia podatku | Sposób obliczenia podatku |
| kwota mniejsza lub równa 85 528 zł | 18% podstawy obliczenia podatku pomniejszone o 556,02 zł |
| kwota większa niż 85 528 zł | 14 839,02 zł plus 32% nadwyżki ponad 85 528 zł |
Uzupełnij zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
W 2016 roku podstawa obliczenia podatku dla pana Kamila wyniosła 94 500 zł. Wysokość podatku (w zł) od dochodu pana Kamila opisuje wyrażenie A/B .
A) 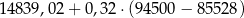 B)
B) 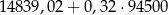
W 2016 roku podstawa obliczenia podatku dla pani Ewy wyniosła 79 300 zł. Wysokość podatku (w zł) od dochodu pani Ewy opisuje wyrażenie C/D .
C) 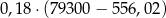 D)
D) 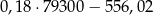
Jeśli 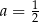 ,
, 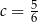 i
i 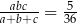 , to
, to 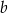 jest równe
jest równe
A)  B)
B)  C)
C) 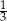 D)
D) 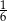
Informacja do zadań 7 i 8
Liczbę ogniw  łańcucha rowerowego można dobrać korzystając ze wzoru
łańcucha rowerowego można dobrać korzystając ze wzoru
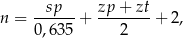
gdzie 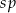 jest odległością w centymetrach od osi suportu do osi tylnej piasty,
jest odległością w centymetrach od osi suportu do osi tylnej piasty, 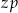 jest liczbą zębów największej zębatki z przodu, a
jest liczbą zębów największej zębatki z przodu, a 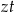 liczbą zębów największej zębatki z tyłu.
liczbą zębów największej zębatki z tyłu.
W tabeli podano niektóre parametry roweru.
| Liczba ogniw łańcucha | 114 |
| Liczba zębów największej zębatki z tyłu | 30 |
| Liczba zębów największej zębatki z przodu | 34 |
Jaka jest odległość osi suportu od osi tylnej piasty w tym rowerze? Wybierz odpowiedź spośród podanych.
A) 50,8 cm B) 48,26 cm C) 46,99 cm D) 45,72 cm
Uzupełnij zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
Jacek w swoim rowerze wymienił przednie zębatki tak, że zmniejszył liczbę zębów największej zębatki z 46 do 42 zębów. Jacek po wymianie zębatek powinien skrócić łańcuch o A/B .
A) 1 ogniwo B) 2 ogniwa
Karol w swoim rowerze wymienił zarówno przednie jak i tylne zębatki w ten sposób, że liczba zębów w każdej z zębatek zwiększyła się o 2. Karol po wymianie zębatek powinien wydłużyć łańcuch o C/D .
C) 1 ogniwo D) 2 ogniwa
Połową odwrotności sześcianu liczby 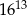 jest
jest
A) 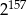 B)
B) 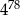 C)
C) 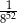 D)
D) 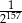
Uzupełnij zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
Wartość wyrażenia 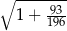 jest równa A/B .
jest równa A/B .
A) 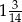 B)
B) 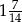
Wartość wyrażenia 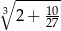 jest równa C/D .
jest równa C/D .
C) 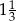 D)
D) 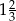
Na festyn przygotowano loterię, w której było 255 losów, w tym 85 wygrywających. Przed rozpoczęciem festynu dołożono jeszcze 30 losów wygrywających i 60 przegrywających. Czy prawdopodobieństwo wyciągnięcia losu wygrywającego w tej loterii zmieniło się po dołożeniu losów? Wybierz odpowiedź T albo N i jej uzasadnienie spośród A, B albo C.
| Tak | Nie |
| ponieważ | |
| A) | różnica liczby losów wygrywających i przegrywających po dołożeniu losów nie jest taka sama jak na początku. |
| B) | dołożono więcej losów przegrywających niż wygrywających. |
| C) | nie zmienił się stosunek liczby losów wygrywających do liczby wszystkich losów. |
Dwa sąsiednie kąty wewnętrzne czworokąta mają miarę  , trzeci ma miarę o
, trzeci ma miarę o 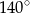 większą niż kąt
większą niż kąt  , a czwarty ma miarę osiem razy większą niż kąt
, a czwarty ma miarę osiem razy większą niż kąt  .
.
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Czworokąt ten jest
A) prostokątem. B) równoległobokiem. C) deltoidem. D) trapezem.
W skład aparatury pomiarowej dwóch urządzeń wchodzą dwie tarcze z obrotowymi wskazówkami (zobacz rysunek).
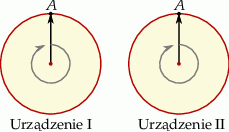
Wskazówki w chwili 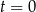 wskazują zaznaczone położenie
wskazują zaznaczone położenie 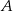 . Następnie obracają się w ten sposób, że wskazówka I urządzenia znajduje się w położeniu
. Następnie obracają się w ten sposób, że wskazówka I urządzenia znajduje się w położeniu 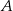 co 6 minut, a wskazówka urządzenia II znajduje się w pozycji
co 6 minut, a wskazówka urządzenia II znajduje się w pozycji 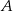 co 8 minut. Ile razy w ciągu 100 minut obserwacji tych tarcz obie wskazówki będą jednocześnie wskazywać położenie
co 8 minut. Ile razy w ciągu 100 minut obserwacji tych tarcz obie wskazówki będą jednocześnie wskazywać położenie 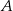 ? Wybierz właściwą odpowiedź spośród podanych.
? Wybierz właściwą odpowiedź spośród podanych.
A) 5 B) 4 C) 8 D) 6
Kacper ma dwa jednakowe klocki w kształcie ostrosłupa prawidłowego sześciokątnego, każdy o polu powierzchni całkowitej 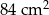 . Podstawa i ściana boczna klocka mają równe pola. Staś skleił oba klocki podstawami tak, jak na rysunku.
. Podstawa i ściana boczna klocka mają równe pola. Staś skleił oba klocki podstawami tak, jak na rysunku.
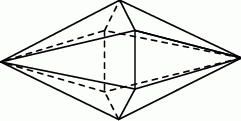
Jakie pole powierzchni ma bryła otrzymana przez Stasia? Wybierz właściwą odpowiedź spośród podanych.
A) 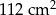 B)
B) 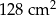 C)
C) 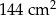 D)
D) 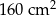
Bok rombu ma długość 26 cm, a jedna z jego przekątnych ma długość 48 cm. Pole tego rombu jest równe
A) 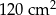 B)
B) 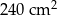 C)
C) 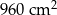 D)
D) 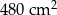
Asia ma w skarbonce 82 zł. Najwięcej w skarbonce jest złotówek, dwa razy więcej niż dwuzłotówek, a cztery razy więcej niż pięciozłotówek. Pozostałe monety w skarbonce to pięćdziesięciogroszówki, których liczba stanowi 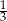 liczby złotówek. Ile było złotówek w skarbonce?
liczby złotówek. Ile było złotówek w skarbonce?
Motocyklista i rowerzysta jeżdżą po zamkniętym torze w tym samym kierunku. Schemat tego toru został przedstawiony kwadratowej siatce.
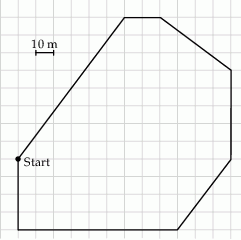
Motocyklista dubluje rowerzystę co 25 s. Z jaką prędkością jedzie każdy z nich, jeśli motocyklista jedzie 3 razy szybciej od rowerzysty?
Kamil miał cukierki w dwóch smakach – orzechowe i miętowe. Początkowo cukierków o smaku orzechowym było cztery razy więcej niż cukierków o smaku miętowym. Gdy Kamil zjadł 21 cukierków orzechowych, to okazało się, że cukierków miętowych jest dwa razy więcej niż orzechowych. Ile cukierków miętowych miał Kamil?
Dany jest prostokąt 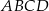 o wymiarach 10 cm i 24 cm. Odcinek
o wymiarach 10 cm i 24 cm. Odcinek 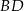 jest przekątną tego prostokąta. Odcinek
jest przekątną tego prostokąta. Odcinek 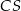 jest wysokością trójkąta
jest wysokością trójkąta  (patrz rysunek).
(patrz rysunek).
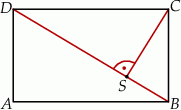
Oblicz długość odcinka 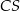 .
.

