/Szkoła podstawowa/Egzamin ósmoklasisty/Egzamin 2022
Próbny Egzamin Ósmoklasisty
z Matematyki Zestaw przygotowany przez serwis zadania.info 9 kwietnia 2022 Czas pracy: 100 minut
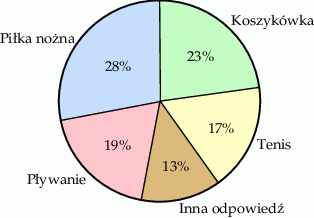
Grupie dwustu osób zadano pytanie: „Jaka jest twoja ulubiona dyscyplina sportu?”. Wyniki tej ankiety przedstawiono na wykresie.
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Z informacji podanych na diagramie wynika, że:
A) 28 osób jako ulubioną dyscyplinę podało piłkę nożną.
B) Łączna liczba odpowiedzi: „piłka nożna” i „tenis” jest równa liczbie wszystkich pozostałych odpowiedzi.
C) Liczba odpowiedzi „pływanie” była o 4 większa od liczby odpowiedzi „tenis”.
D) Liczba odpowiedzi „tenis” była o 6 mniejsza od liczby odpowiedzi „koszykówka”.
Dane są cztery liczby 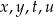 zapisane za pomocą wyrażeń arytmetycznych:
zapisane za pomocą wyrażeń arytmetycznych:
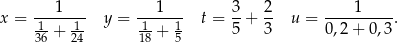
Która z tych liczb jest najmniejsza? Wybierz właściwą odpowiedź spośród podanych.
A)  B)
B) 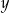 C)
C) 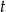 D)
D) 
Cenę roweru podwyższono najpierw o 35%, a później o 150 zł. Po obu podwyżkach rower kosztuje 4200 zł.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Przed tymi dwoma podwyżkami rower kosztował 3200 zł. | P | F |
| Po obu podwyżkach cena roweru stanowi 140% ceny początkowej. | P | F |
Z reguł działań na potęgach wynika, że:
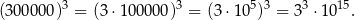
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. Z tych samych reguł wynika, że liczba 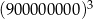 jest równa
jest równa
A) 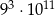 B)
B) 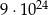 C)
C) 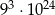 D)
D) 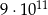
Glazurnik układał płytki. Wykres przedstawia liczbę ułożonych płytek w zależności od czasu w trakcie ośmiogodzinnego dnia pracy.
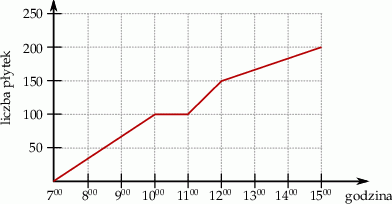
Na podstawie wykresu wybierz zdanie fałszywe.
A) O godzinie 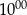 glazurnik rozpoczął godzinną przerwę.
glazurnik rozpoczął godzinną przerwę.
B) Od 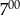 do
do 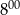 glazurnik ułożył mniej płytek niż od
glazurnik ułożył mniej płytek niż od 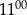 do
do 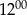 .
.
C) W ciągu każdej godziny glazurnik układał taką samą liczbę płytek.
D) Przez ostatnie trzy godziny pracy glazurnik ułożył 50 płytek.
Czy suma dowolnych trzech kolejnych liczb całkowitych jest podzielna przez 3? Wybierz odpowiedź T (tak) albo N (nie) i jej uzasadnienie spośród oznaczonych literami A–C.
| Tak | Nie |
| ponieważ wśród dowolnych trzech kolejnych liczb całkowitych | |
| A) | musi znajdować się liczba podzielna przez 3. |
| B) | znajdują się liczby, które dają reszty: 0, 1 i 2 przy dzieleniu przez 3. |
| C) | znajduje się liczba, która nie jest podzielna przez 3. |
Zależność między liczbą przekątnych (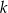 ) a liczbą boków (
) a liczbą boków ( ) wielokąta wypukłego określa wzór
) wielokąta wypukłego określa wzór 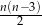 . Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Liczba przekątnych w dwunastokącie wypukłym jest sześć razy większa od liczby przekątnych w sześciokącie wypukłym. | P | F |
| Liczba przekątnych w siedmiokącie wypukłym jest o 10 większa od liczby przekątnych w czworokącie wypukłym. | P | F |
Od liczby 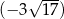 odejmujemy liczbę
odejmujemy liczbę 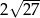 .
.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Otrzymany wynik jest liczbą
A) większą od 1.
B) dodatnią mniejszą od 1.
C) mniejszą od 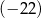 .
.
D) ujemną większą od 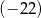 .
.
Łukasz wyciął z kartki papieru trójkąt równoramienny 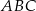 , a następnie zagiął w nim dwa narożniki tak, że wierzchołki
, a następnie zagiął w nim dwa narożniki tak, że wierzchołki 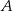 i
i 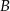 trójkąta znalazły się w środku
trójkąta znalazły się w środku 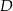 jego podstawy. Powstał w ten sposób pięciokąt
jego podstawy. Powstał w ten sposób pięciokąt 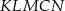 .
.
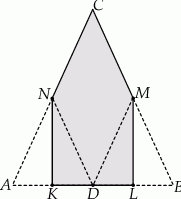
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Pole pięciokąta 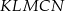 stanowi 75% pola trójkąta stanowi 75% pola trójkąta 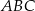 . . | P | F |
Obwód pięciokąta 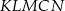 jest taki sam jak obwód trójkąta jest taki sam jak obwód trójkąta 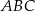 . . | P | F |
Kasia kupiła cztery ołówki i długopis. Średnia arytmetyczna cen tych pięciu artykułów była równa 1,8 zł. Ołówki kosztowały łącznie 6 zł. Ile kosztował długopis? Wybierz właściwą odpowiedź spośród podanych.
A) 2,7 zł B) 1,5 zł C) 2 zł D) 3 zł
W pewnej loterii przygotowano 20 losów wygrywających i pewną liczbę losów przegrywających. W trakcie losowania wyciągnięto 20 losów i wszystkie były przegrywające. Po wyciągnięciu tych 20 losów prawdopodobieństwo wyciągnięcia losu wygrywającego wzrosło do 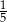 .
.
Uzupełnij zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
Na loterię przygotowano A/B losów przegrywających.
A) 80 B) 100
Wyciągnięto kolejnych 10 losów przegrywających. Zatem prawdopodobieństwo wyciągnięcia losu wygrywającego wzrosło do C/D .
C)  D)
D) 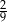
W trójkącie równoramiennym 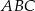 o podstawie
o podstawie 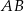 narysowano wysokość
narysowano wysokość 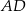 , jak na rysunku. Kąt między tą wysokością a podstawą
, jak na rysunku. Kąt między tą wysokością a podstawą 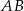 jest równy
jest równy 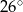 .
.
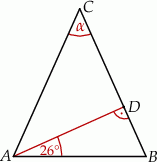
Jaką miarę ma kąt  zaznaczony na rysunku? Wybierz właściwą odpowiedź spośród podanych.
zaznaczony na rysunku? Wybierz właściwą odpowiedź spośród podanych.
A) 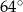 B)
B) 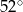 C)
C) 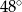 D)
D) 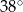
Skrzynia ma kształt prostopadłościanu. Podłoga skrzyni ma wymiary 2,4 m i 1,5 m, a wysokość skrzyni jest równa 1 m. Piasek wsypany do skrzyni zajmuje 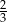 jej pojemności. Ile metrów sześciennych piasku wsypano do skrzyni? Wybierz właściwą odpowiedź spośród podanych.
jej pojemności. Ile metrów sześciennych piasku wsypano do skrzyni? Wybierz właściwą odpowiedź spośród podanych.
A) 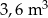 B)
B) 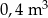 C)
C) 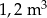 D)
D) 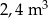
Prostokąt 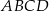 podzielono odcinkiem
podzielono odcinkiem 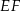 na dwa prostokąty. Odcinek
na dwa prostokąty. Odcinek 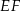 ma długość 12 cm, a odcinek
ma długość 12 cm, a odcinek 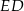 ma długość 2 cm. Pole prostokąta
ma długość 2 cm. Pole prostokąta 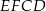 stanowi
stanowi 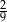 pola prostokąta
pola prostokąta 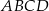 .
.

Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Pole prostokąta 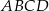 jest równe jest równe 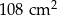 . . | P | F |
Odcinek 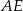 ma długość 7 cm. ma długość 7 cm. | P | F |
Na rysunku przedstawiono bryłę zbudowaną z sześciu jednakowych sześcianów. Objętość tej bryły jest równa 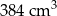 .
.
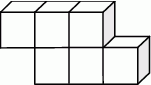
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Pole powierzchni całkowitej tej bryły jest równe
A) 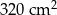 B)
B) 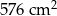 C)
C) 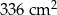 D)
D) 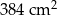
Asi zerwał się naszyjnik. Trzecią część liczby korali znalazła na podłodze, jedną czwartą w kieszeni, jedną piątą pod oparciem kanapy, a szósta część liczby korali została na sznurku. Sześciu korali nie udało się jej odnaleźć. Oblicz, ile korali zostało na sznurku.
Na rysunku pokazano plan dwóch dróg, którymi Olek chodzi do szkoły.
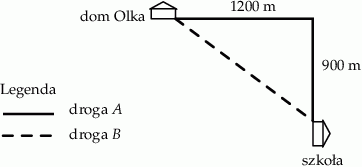
Przyjmij, że Olek porusza się ze stałą prędkością 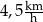 . Oblicz, o ile minut krócej Olek idzie do szkoły drogą
. Oblicz, o ile minut krócej Olek idzie do szkoły drogą 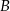 niż drogą
niż drogą 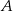 .
.
Adrian chciał kupić 12 jednakowych butelek soku owocowego, ale zabrakło mu 23,80 złotych. Kupił więc 8 butelek soku i zostało mu 5,80 złotego. Ile kosztuje jedna butelka tego soku?
W prostokącie 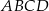 o polu
o polu 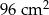 bok
bok 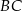 ma długość 8 cm. Na bokach
ma długość 8 cm. Na bokach 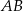 i
i 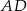 wybrano punkty
wybrano punkty 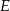 i
i 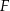 tak, że
tak, że 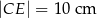 i
i 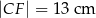 . Oblicz pole czworokąta
. Oblicz pole czworokąta 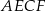 .
.