/Szkoła średnia/Zadania maturalne/Matura 2022/Matura próbna
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis zadania.info poziom podstawowy 12 marca 2022 Czas pracy: 170 minut
Zadania zamknięte
Liczba 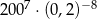 jest równa
jest równa
A) 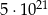 B)
B) 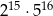 C)
C) 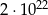 D)
D) 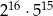
Cena telewizora po 3 podwyżkach o 25% i dwóch obniżkach o 20% wzrosła o 1200 zł. Nowa cena telewizora jest równa
A) 4800 zł B) 5760 zł C) 6000 zł D) 4500 zł
Niech 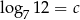 . Wtedy
. Wtedy 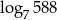 jest równy
jest równy
A) 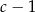 B)
B)  C)
C) 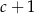 D)
D) 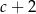
Wyrażenie 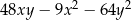 może być przekształcone do postaci
może być przekształcone do postaci
A) 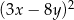 B)
B) 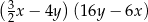 C)
C) 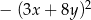 D)
D) 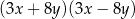
Różnica 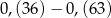 jest równa
jest równa
A) 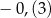 B)
B) 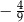 C)
C) 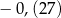 D)
D) 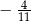
Na rysunku 1 jest przedstawiony wykres funkcji 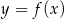 .
.
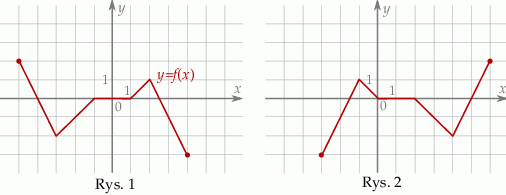
Funkcja przedstawiona na rysunku 2 jest określona wzorem
A) 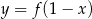 B)
B) 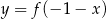 C)
C) 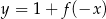 D)
D) 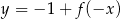
Zbiór wszystkich liczb rzeczywistych spełniających nierówność 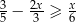 jest przedziałem
jest przedziałem
A) 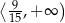 B)
B) 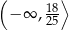 C)
C) 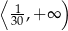 D)
D) 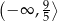
Funkcja 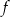 jest określona wzorem
jest określona wzorem 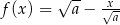 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Miejscem zerowym tej funkcji jest liczba 8. Wtedy
. Miejscem zerowym tej funkcji jest liczba 8. Wtedy
A) 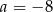 B)
B) 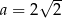 C)
C) 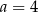 D)
D) 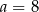
Proste o równaniach 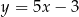 oraz
oraz 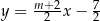 są równoległe, gdy
są równoległe, gdy
A) 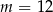 B)
B) 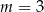 C)
C) 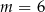 D)
D) 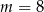
Liczby 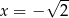 i
i 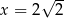 są pierwiastkami równania
są pierwiastkami równania
A) 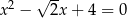 B)
B) 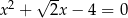
C) 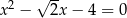 D)
D) 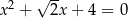
Na rysunku przedstawiono fragmenty dwóch wykresów: funkcji liniowej 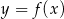 i funkcji
i funkcji ![2 y = g(x ) = [f(x)]](https://img.zadania.info/zes/0065316/HzesT52x.gif) . Oba wykresy przechodzą przez punkty o współrzędnych
. Oba wykresy przechodzą przez punkty o współrzędnych 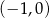 i
i 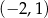 .
.
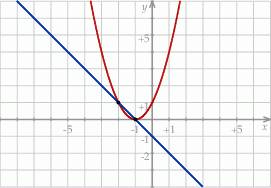
Zbiorem wartości funkcji 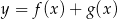 jest przedział
jest przedział
A) 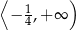 B)
B) 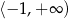 C)
C) 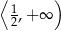 D)
D) 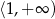
Wykresem funkcji kwadratowej 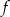 określonej wzorem
określonej wzorem 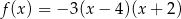 jest parabola o wierzchołku
jest parabola o wierzchołku 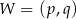 . Współrzędne wierzchołka
. Współrzędne wierzchołka 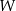 spełniają warunki
spełniają warunki
A) 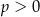 i
i 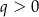 B)
B) 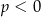 i
i 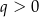 C)
C) 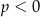 i
i 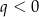 D)
D) 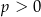 i
i 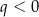
Czterowyrazowy ciąg 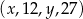 jest geometryczny i wszystkie jego wyrazy są dodatnie. Stąd wynika, że
jest geometryczny i wszystkie jego wyrazy są dodatnie. Stąd wynika, że
A) 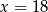 B)
B) 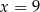 C)
C) 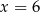 D)
D) 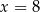
Punkt 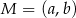 jest środkiem odcinka o końcach
jest środkiem odcinka o końcach 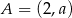 i
i 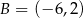 . Wówczas
. Wówczas
A) 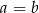 B)
B) 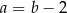 C)
C) 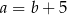 D)
D) 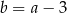
Liczba 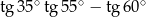 jest równa
jest równa
A) 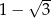 B)
B) 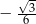 C)
C) 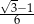 D)
D) 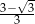
Jeżeli 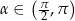 i
i 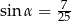 , to
, to
A) 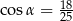 B)
B) 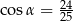 C)
C) 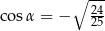 D)
D) 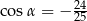
Prosta 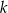 jest styczna w punkcie
jest styczna w punkcie 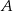 do okręgu o środku
do okręgu o środku 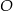 . Punkt
. Punkt 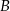 leży na tym okręgu i miara kąta
leży na tym okręgu i miara kąta 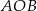 jest równa
jest równa 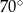 . Przez punkty
. Przez punkty 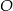 i
i 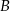 poprowadzono prostą, która przecina prostą
poprowadzono prostą, która przecina prostą 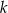 w punkcie
w punkcie 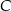 (zobacz rysunek).
(zobacz rysunek).
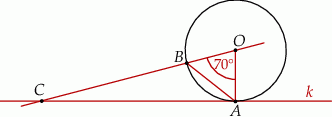
Miara kąta 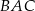 jest równa
jest równa
A) 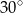 B)
B) 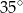 C)
C) 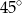 D)
D) 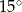
Miary kątów trójkąta tworzą ciąg arytmetyczny o pierwszym wyrazie 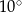 . Różnica tego ciągu jest równa
. Różnica tego ciągu jest równa
A) 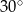 B)
B) 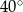 C)
C) 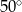 D)
D) 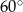
Dany jest trójkąt prostokątny 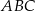 o bokach
o bokach 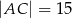 ,
, 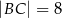 ,
, 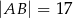 . Dwusieczne kątów tego trójkąta przecinają się w punkcie
. Dwusieczne kątów tego trójkąta przecinają się w punkcie 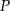 (zobacz rysunek).
(zobacz rysunek).
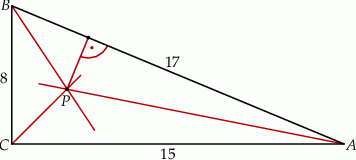
Odległość  punktu
punktu 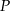 od przeciwprostokątnej
od przeciwprostokątnej 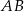 jest równa
jest równa
A) 2 B) 4 C)  D) 3
D) 3
Punkt 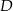 jest środkiem podstawy trójkąta równoramiennego
jest środkiem podstawy trójkąta równoramiennego 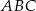 , w którym
, w którym 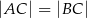 . Odległość punktu
. Odległość punktu 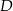 od prostej
od prostej 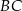 jest równa 12, a długość odcinka
jest równa 12, a długość odcinka 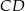 jest równa 20.
jest równa 20.
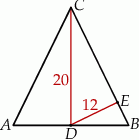
Podstawa 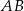 trójkąta
trójkąta 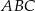 ma długość
ma długość
A) 15 B) 30 C) 24 D) 16
Pole powierzchni jednej ze ścian aluminiowej kostki do gry jest równe 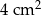 . Gęstość aluminium jest równa ok.
. Gęstość aluminium jest równa ok. 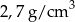 . Masa kostki jest równa około
. Masa kostki jest równa około
A) 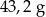 B)
B) 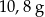 C)
C) 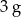 D)
D) 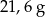
Punkty 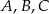 i
i 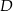 leżą na okręgu o środku
leżą na okręgu o środku 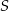 . Miary kątów
. Miary kątów 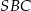 ,
, 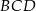 ,
, 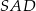 są równe odpowiednio:
są równe odpowiednio: 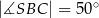 ,
, 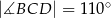 ,
, 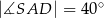 (zobacz rysunek).
(zobacz rysunek).
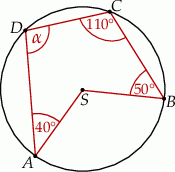
Wynika stąd, że miara  kąta
kąta 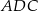 jest równa
jest równa
A) 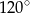 B)
B) 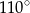 C)
C) 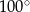 D)
D) 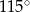
Obrazem prostej o równaniu 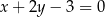 w symetrii osiowej względem osi
w symetrii osiowej względem osi 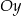 jest prosta o równaniu
jest prosta o równaniu
A) 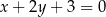 B)
B) 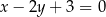 C)
C) 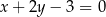 D)
D) 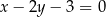
Każda krawędź graniastosłupa prawidłowego sześciokątnego ma długość równą 3 (zobacz rysunek).
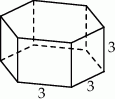
Pole powierzchni całkowitej tego graniastosłupa jest równe
A) 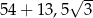 B)
B) 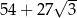 C)
C) 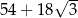 D)
D) 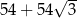
Punkt 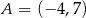 jest wierzchołkiem kwadratu
jest wierzchołkiem kwadratu 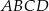 , a punkt
, a punkt 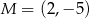 jest punktem przecięcia się przekątnych tego kwadratu. Wynika stąd, że pole kwadratu
jest punktem przecięcia się przekątnych tego kwadratu. Wynika stąd, że pole kwadratu 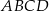 jest równe
jest równe
A) 360 B) 90 C) 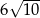 D)
D) 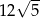
Rysunek przedstawia ostrosłup prawidłowy czworokątny 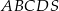 .
.
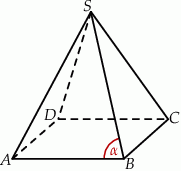
Stosunek pola powierzchni bocznej tego ostrosłupa do pola jego podstawy jest równy 4. Zatem tangens zaznaczonego kąta 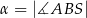 jest równy
jest równy
A) 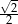 B)
B) 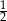 C) 2 D) 4
C) 2 D) 4
Losujemy jedną liczbę ze zbioru 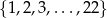 . Niech
. Niech 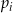 oznacza prawdopodobieństwo otrzymania liczby dającej resztę
oznacza prawdopodobieństwo otrzymania liczby dającej resztę 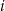 przy dzieleniu przez 4. Wtedy
przy dzieleniu przez 4. Wtedy
A) 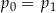 B)
B) 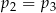 C)
C) 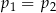 D)
D) 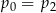
Ciąg 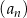 jes określony wzorem
jes określony wzorem 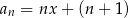 dla
dla 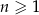 i pewnej liczby rzeczywistej
i pewnej liczby rzeczywistej  . Średnia arytmetyczna pierwszych ośmiu wyrazów tego ciągu jest równa 19. Wtedy
. Średnia arytmetyczna pierwszych ośmiu wyrazów tego ciągu jest równa 19. Wtedy  jest równe
jest równe
A) 3 B) 1,5 C) 27 D) 6
Zadania otwarte
Rozwiąż nierówność 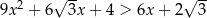 .
.
Wykaż, że dla wszystkich liczb rzeczywistych 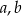 i
i  takich, że
takich, że 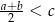 i
i 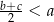 , prawdziwa jest nierówność
, prawdziwa jest nierówność
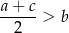
Oblicz sumę wszystkich liczb mniejszych od 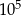 , które mogą być zapisane w postaci
, które mogą być zapisane w postaci 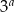 dla pewnej nieujemnej liczby całkowitej
dla pewnej nieujemnej liczby całkowitej  .
.
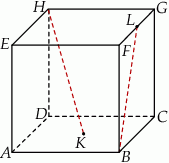
Punkty 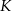 i
i 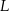 są środkami odpowiednio podstawy
są środkami odpowiednio podstawy 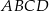 i krawędzi
i krawędzi 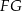 sześcianu
sześcianu 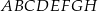 . Suma kwadratów długości odcinków
. Suma kwadratów długości odcinków 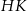 i
i 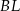 jest równa 44. Oblicz objętość tego sześcianu.
jest równa 44. Oblicz objętość tego sześcianu.
Trójkąt równoboczny 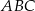 ma pole równe
ma pole równe 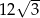 . Prosta równoległa do boku
. Prosta równoległa do boku 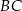 przecina boki
przecina boki 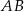 i
i 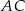 – odpowiednio – w punktach
– odpowiednio – w punktach 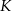 i
i 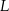 . Stosunek obwodów trójkątów
. Stosunek obwodów trójkątów 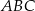 i
i 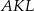 jest równy
jest równy 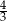 . Oblicz długość boku trójkąta
. Oblicz długość boku trójkąta 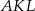 .
.
Doświadczenie losowe polega na dwukrotnym rzucie symetryczną sześcienną kostką do gry. Oblicz prawdopodobieństwo zdarzenia 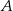 polegającego na tym, że iloczyn liczb oczek wyrzuconych w dwóch rzutach będzie podzielny przez 6.
polegającego na tym, że iloczyn liczb oczek wyrzuconych w dwóch rzutach będzie podzielny przez 6.
Podstawa 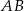 trójkąta równoramiennego
trójkąta równoramiennego 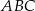 jest zawarta w prostej o równaniu
jest zawarta w prostej o równaniu 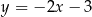 . Wierzchołki
. Wierzchołki 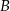 i
i 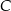 mają współrzędne
mają współrzędne 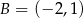 i
i 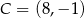 . Oblicz współrzędne wierzchołka
. Oblicz współrzędne wierzchołka 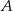 i pole trójkąta
i pole trójkąta 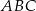 .
.

