/Szkoła średnia/Zadania maturalne/Matura 2022/Matura próbna
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis zadania.info poziom podstawowy 26 marca 2022 Czas pracy: 170 minut
Zadania zamknięte
W trakcie testów drogowych samochód numer 1 poruszał się ze stałą prędkością 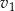 i pokonał trasę o 10% dłuższą, niż samochód nr 2, który poruszał się ze stałą prędkością
i pokonał trasę o 10% dłuższą, niż samochód nr 2, który poruszał się ze stałą prędkością 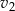 . Czas w jakim samochód nr 2 pokonał swoją trasę był o 20% krótszy, niż czas w jakim swoją trasę pokonał samochód nr 1. Stosunek prędkości
. Czas w jakim samochód nr 2 pokonał swoją trasę był o 20% krótszy, niż czas w jakim swoją trasę pokonał samochód nr 1. Stosunek prędkości 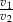 jest równy
jest równy
A) 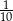 B)
B)  C)
C) 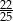 D)
D) 
Liczba 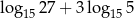 jest równa
jest równa
A) 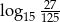 B) 3 C) 2 D)
B) 3 C) 2 D) 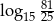
Rozważamy przedziały liczbowe: 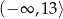 i
i 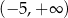 . Ile jest wszystkich liczb całkowitych, które należą jednocześnie do obu rozważanych przedziałów?
. Ile jest wszystkich liczb całkowitych, które należą jednocześnie do obu rozważanych przedziałów?
A) 17 B) 16 C) 18 D) 19
Liczba 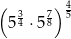 jest równa
jest równa
A) 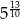 B)
B) 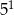 C)
C) 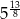 D)
D) 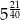
Wyrażenie 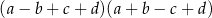 może być zapisane w postaci
może być zapisane w postaci
A) 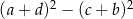 B)
B) 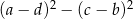
C) 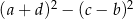 D)
D) 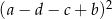
Zbiór rozwiązań nierówności 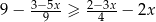 jest taki sam jak zbiór rozwiązań nierówności
jest taki sam jak zbiór rozwiązań nierówności
A) 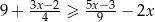 B)
B) 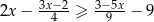
C) 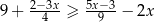 D)
D) 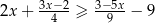
Na poniższym rysunku przedstawiono wykres funkcji 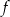 określonej w zbiorze
określonej w zbiorze 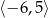 .
.
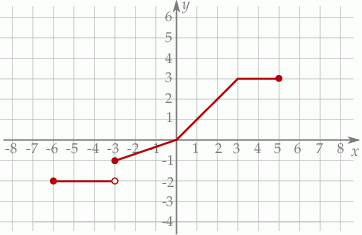
Funkcja 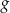 jest określona wzorem
jest określona wzorem 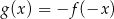 dla
dla 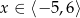 . Wskaż zdanie prawdziwe.
. Wskaż zdanie prawdziwe.
A) Zbiór wartości funkcji 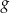 nie zawiera liczb dodatnich.
nie zawiera liczb dodatnich.
B) Punkt 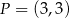 należy do wykresów funkcji
należy do wykresów funkcji 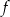 i
i 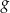 .
.
C) Równanie 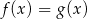 ma nieskończenie wiele rozwiązań.
ma nieskończenie wiele rozwiązań.
D) Jest tylko jedna liczba  spełniająca nierówność
spełniająca nierówność 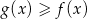 .
.
Równanie 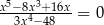
A) ma dwa rozwiązania B) ma trzy rozwiązania
C) nie ma rozwiązań D) ma jedno rozwiązanie
Liczba dzielników naturalnych liczby 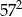 jest równa
jest równa
A) 8 B) 9 C) 16 D) 4
Funkcja kwadratowa 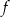 jest określona wzorem
jest określona wzorem 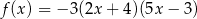 . Wierzchołek paraboli, która jest wykresem funkcji
. Wierzchołek paraboli, która jest wykresem funkcji 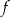 , ma współrzędną
, ma współrzędną  równą
równą
A) 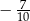 B)
B) 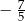 C)
C) 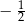 D)
D) 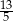
Do wykresu funkcji 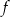 określonej dla każdej liczby rzeczywistej
określonej dla każdej liczby rzeczywistej  wzorem
wzorem 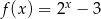 należy punkt o współrzędnych
należy punkt o współrzędnych
A) 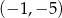 B)
B) 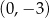 C)
C) 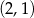 D)
D) 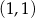
Kąt  jest ostry i
jest ostry i 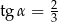 . Wtedy
. Wtedy
A) 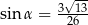 B)
B) 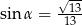 C)
C) 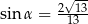 D)
D) 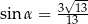
Dane są ciągi 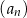 ,
, 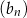 ,
, 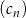 ,
, 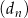 , określone dla każdej liczby naturalnej
, określone dla każdej liczby naturalnej 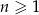 wzorami:
wzorami: 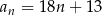 ,
, 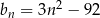 ,
, 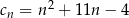 ,
, 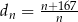 . Liczba 206 jest dziesiątym wyrazem ciągu
. Liczba 206 jest dziesiątym wyrazem ciągu
A) 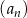 B)
B) 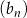 C)
C) 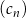 D)
D) 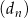
Najmniejszą liczbą całkowitą należącą do dziedziny funkcji 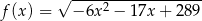 jest
jest
A) 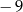 B)
B) 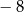 C)
C) 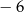 D)
D) 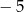
Ciąg arytmetyczny 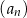 jest określony dla każdej liczby naturalnej
jest określony dla każdej liczby naturalnej 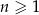 . Piąty wyraz tego ciągu jest o 12 większy od trzeciego wyrazu. Wtedy różnica
. Piąty wyraz tego ciągu jest o 12 większy od trzeciego wyrazu. Wtedy różnica 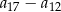 jest równa
jest równa
A) 60 B) 6 C) 30 D) 24
W rosnącym ciągu geometrycznym 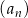 , określonym dla
, określonym dla 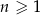 , pierwsze trzy wyrazy są długościami boków trójkąta prostokątnego. Zatem
, pierwsze trzy wyrazy są długościami boków trójkąta prostokątnego. Zatem
A) 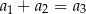 B)
B) 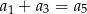 C)
C) 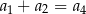 D)
D) 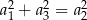
Punkty 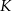 i
i 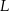 są punktami styczności okręgu wpisanego w trapez równoramienny
są punktami styczności okręgu wpisanego w trapez równoramienny 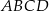 z bokami
z bokami 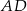 i
i 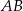 . Kąt ostry tego trapezu ma miarę
. Kąt ostry tego trapezu ma miarę 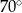 (zobacz rysunek).
(zobacz rysunek).
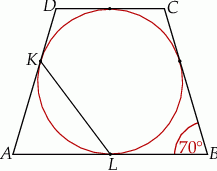
Miara kąta 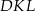 jest równa
jest równa
A) 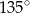 B)
B) 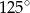 C)
C) 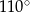 D)
D) 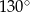
Okrąg o środku w punkcie 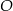 jest wpisany w trójkąt
jest wpisany w trójkąt 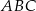 . Wiadomo, że
. Wiadomo, że 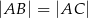 i
i 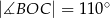 (zobacz rysunek).
(zobacz rysunek).
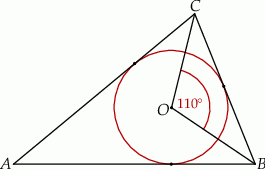
Miara kąta 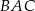 jest równa
jest równa
A) 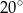 B)
B) 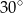 C)
C) 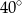 D)
D) 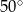
Pole pewnego trójkąta równobocznego jest równe 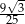 . Obwód tego trójkąta jest równy
. Obwód tego trójkąta jest równy
A) 4 B) 2 C) 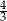 D)
D) 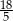
Na okręgu o środku w punkcie 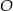 leżą punkty
leżą punkty 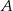 ,
, 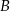 oraz
oraz 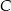 . Odcinek
. Odcinek 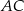 jest średnicą tego okręgu, a kąt środkowy
jest średnicą tego okręgu, a kąt środkowy 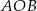 ma miarę
ma miarę 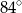 (zobacz rysunek).
(zobacz rysunek).
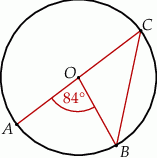
Miara kąta 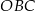 jest równa
jest równa
A) 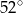 B)
B) 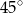 C)
C) 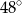 D)
D) 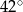
Prosta przechodząca przez punkty 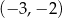 oraz
oraz 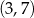 ma równanie
ma równanie
A) 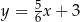 B)
B) 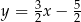 C)
C) 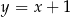 D)
D) 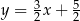
Punkty 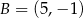 i
i 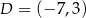 są wierzchołkami rombu
są wierzchołkami rombu 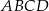 . Współczynnik kierunkowy przekątnej
. Współczynnik kierunkowy przekątnej 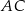 tego rombu jest równy
tego rombu jest równy
A) 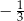 B) 3 C)
B) 3 C) 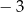 D)
D) 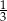
W każdym  –kącie wypukłym (
–kącie wypukłym (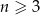 ) liczba przekątnych jest równa
) liczba przekątnych jest równa 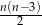 . Jeżeli graniastosłup prosty ma
. Jeżeli graniastosłup prosty ma 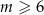 wierzchołków, to liczba wszystkich przekątnych jego podstaw i ścian bocznych jest równa
wierzchołków, to liczba wszystkich przekątnych jego podstaw i ścian bocznych jest równa
A) 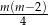 B)
B) 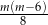 C)
C) 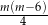 D)
D) 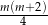
Przeciwległe wierzchołki kwadratu mają współrzędne 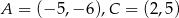 . Promień okręgu wpisanego w ten kwadrat jest równy
. Promień okręgu wpisanego w ten kwadrat jest równy
A) 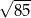 B)
B) 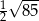 C)
C) 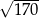 D)
D) 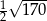
Przekątna sześcianu jest równa 9. Wynika stąd, że objętość tego sześcianu jest równa
A) 243 B) 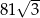 C)
C) 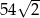 D)
D) 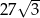
Rzucając wielokrotnie symetryczną kostką do gry otrzymano następujące liczby oczek
| Liczba oczek | 1 | 2 | 3 | 4 | 5 | 6 |
| Liczba wyników | 1 | 4 | 3 | 5 | 4 | 3 |
Średnia liczba oczek otrzymana w jednym rzucie jest równa.
A) 4 B) 3,8 C) 3,5 D) 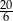
Wszystkich liczb naturalnych trzycyfrowych, mniejszych od 600, w których każda cyfra należy do zbioru 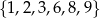 i żadna cyfra się nie powtarza, jest
i żadna cyfra się nie powtarza, jest
A) 108 B) 60 C) 40 D) 299
W pudełku znajdują się płytki z literami i cyframi. Na każdej płytce jest wydrukowana albo jedna wielka litera, albo jedna mała litera, albo jedna cyfra. Płytek z wielkimi literami jest o 25% mniej niż płytek z cyframi, a płytek z małymi literami jest o 40% więcej niż płytek z wielkimi literami. Losujemy jedną płytkę. Prawdopodobieństwo wylosowania płytki z cyfrą jest równe
A) 0,85 B) 0,1 C) 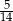 D)
D) 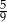
Zadania otwarte
Rozwiąż nierówność: 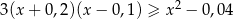 .
.
Udowodnij, że liczba 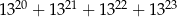 jest podzielna przez 35.
jest podzielna przez 35.
Rozwiąż równanie
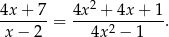
Prosta o równaniu 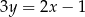 jest osią symetrii wykresu funkcji liniowej
jest osią symetrii wykresu funkcji liniowej 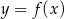 . Ponadto
. Ponadto 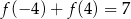 . Wyznacz wzór funkcji
. Wyznacz wzór funkcji 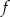 .
.
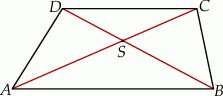
Dany jest trapez 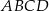 o podstawach
o podstawach 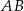 i
i 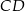 . Przekątne
. Przekątne 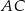 i
i 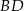 tego trapezu przecinają się w punkcie
tego trapezu przecinają się w punkcie 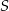 (zobacz rysunek) tak, że
(zobacz rysunek) tak, że 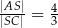 . Pole trójkąta
. Pole trójkąta 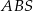 jest równe 24. Oblicz pole trójkąta
jest równe 24. Oblicz pole trójkąta 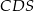 .
.
Ze zbioru wszystkich liczb naturalnych czterocyfrowych, których cyfra tysięcy i cyfra setek należą do zbioru 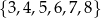 , a cyfra dziesiątek i cyfra jedności należą do zbioru
, a cyfra dziesiątek i cyfra jedności należą do zbioru 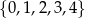 , losujemy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że wylosujemy liczbę czterocyfrową, która jest podzielna przez 4.
, losujemy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że wylosujemy liczbę czterocyfrową, która jest podzielna przez 4.
Punkty 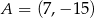 i
i 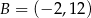 są wierzchołkami trójkąta równoramiennego
są wierzchołkami trójkąta równoramiennego 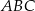 , w którym
, w którym 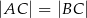 . Wierzchołek
. Wierzchołek 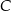 leży na prostej
leży na prostej 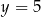 . Oblicz współrzędne wierzchołka
. Oblicz współrzędne wierzchołka 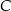 oraz obwód tego trójkąta.
oraz obwód tego trójkąta.

