/Szkoła średnia/Zadania maturalne/Matura 2022/Matura próbna
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis zadania.info poziom rozszerzony 9 kwietnia 2022 Czas pracy: 180 minut
Zadania zamknięte
Liczba 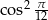 jest równa
jest równa
A) 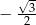 B)
B) 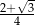 C)
C) 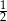 D)
D) 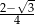
Jeżeli 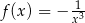 , to
, to
A) 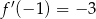 B)
B) 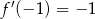 C)
C) 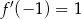 D)
D) 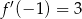
Wektory ![→ a = [m − 2,m + 7]](https://img.zadania.info/zes/0084663/HzesT10x.gif) oraz
oraz ![→ b = [m,2 ]](https://img.zadania.info/zes/0084663/HzesT11x.gif) są równoległe wtedy i tylko wtedy, gdy
są równoległe wtedy i tylko wtedy, gdy
A) 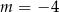 lub
lub 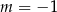 B)
B) 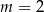 lub
lub 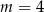
C) 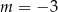 lub
lub 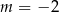 D)
D) 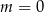
Wielomian 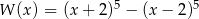 zapisano w postaci
zapisano w postaci 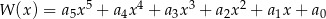 . Suma
. Suma 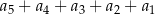 jest równa
jest równa
A) 180 B) 244 C) 242 D) 212
Zadania otwarte
Oblicz granicę 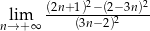 .
.
Uzasadnij, że 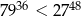 .
.
Rozwiąż nierówność 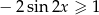 w przedziale
w przedziale 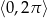 .
.
W trójkącie 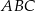 poprowadzono odcinki
poprowadzono odcinki 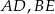 i
i 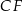 w ten sposób, że punkty
w ten sposób, że punkty 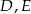 i
i 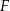 są środkami odpowiednio odcinków
są środkami odpowiednio odcinków 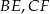 i
i 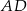 . Wykaż, że pole trójkąta
. Wykaż, że pole trójkąta 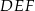 jest siedem razy mniejsze od pola trójkąta
jest siedem razy mniejsze od pola trójkąta 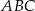 .
.
Wyznacz maksymalne przedziały monotoniczności funkcji 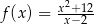 określonej dla
określonej dla 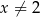 .
.
Dane są liczby dodatnie  i
i 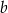 , dla których ciąg
, dla których ciąg 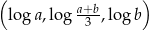 jest rosnącym ciągiem arytmetycznym. Oblicz różnicę tego ciągu.
jest rosnącym ciągiem arytmetycznym. Oblicz różnicę tego ciągu.
Dany jest trójkąt prostokątny 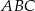 . Przeciwprostokątna tego trójkąta jest 6,5 razy dłuższa niż promień okręgu wpisanego w ten trójkąt. Oblicz sinus tego z kątów ostrych trójkąta
. Przeciwprostokątna tego trójkąta jest 6,5 razy dłuższa niż promień okręgu wpisanego w ten trójkąt. Oblicz sinus tego z kątów ostrych trójkąta 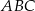 , który ma mniejszą miarę.
, który ma mniejszą miarę.
Ze zbioru wszystkich liczb naturalnych czterocyfrowych losujemy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że wylosowana liczba jest podzielna przez 4 lub 9, jeśli wiadomo, że jest ona podzielna przez 6.
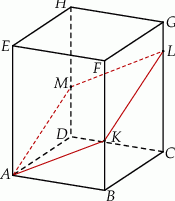
Podstawą graniastosłupa prostego 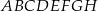 jest romb o boku długości 5, polu 24 i kącie ostrym
jest romb o boku długości 5, polu 24 i kącie ostrym 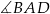 . Graniastosłup ten przecięto płaszczyzną
. Graniastosłup ten przecięto płaszczyzną 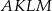 w ten sposób, że otrzymany przekrój jest rombem o kącie ostrym
w ten sposób, że otrzymany przekrój jest rombem o kącie ostrym 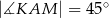 (zobacz rysunek). Oblicz pole tego przekroju.
(zobacz rysunek). Oblicz pole tego przekroju.
W trójkącie równoramiennym 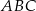 dane są wierzchołki podstawy:
dane są wierzchołki podstawy: 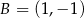 i
i 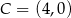 . Jedno z ramion trójkąta zawiera się w prostej o równaniu
. Jedno z ramion trójkąta zawiera się w prostej o równaniu 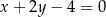 . Na boku
. Na boku 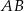 tego trójkąta obrano taki punkt
tego trójkąta obrano taki punkt 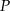 , że
, że 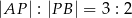 . Napisz równanie okręgu o środku w punkcie
. Napisz równanie okręgu o środku w punkcie 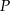 , stycznego do podstawy
, stycznego do podstawy 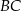 .
.
Rozpatrujemy wszystkie prostokąty 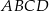 , w których suma długości dwóch sąsiednich boków i przekątnej jest równa 6. Niech
, w których suma długości dwóch sąsiednich boków i przekątnej jest równa 6. Niech 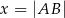 .
.
- Wykaż, że pole
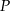 prostokąta
prostokąta 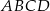 jako funkcja zmiennej
jako funkcja zmiennej  jest określone wzorem
jest określone wzorem 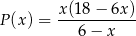
- Wyznacz dziedzinę funkcji
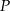 .
. - Oblicz długości boków tego z rozpatrywanych prostokątów, który ma największe pole. Oblicz to największe pole.

