/Szkoła średnia/Zadania maturalne/Matura 2022/Matura próbna/Zadania.info
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis zadania.info poziom rozszerzony 26 marca 2022 Czas pracy: 180 minut
Zadania zamknięte
W turnieju szachowym rozegrano 28 partii. Każdy zawodnik rozegrał z każdym dokładnie 1 mecz. Ilu zawodników brało udział w turnieju?
A) 10 B) 9 C) 8 D) 7
Okrąg jest styczny do boku 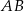 trójkąta
trójkąta 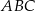 w punkcie
w punkcie 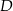 oraz przecina boki
oraz przecina boki 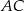 i
i 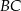 tego trójkąta odpowiednio w punktach
tego trójkąta odpowiednio w punktach 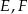 i
i 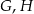 (zobacz rysunek). Kat
(zobacz rysunek). Kat 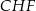 ma miarę
ma miarę 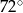 .
.
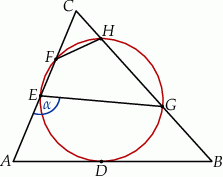
Zaznaczony na rysunku kąt  ma miarę
ma miarę
A) 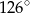 B)
B) 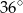 C)
C) 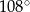 D)
D) 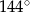
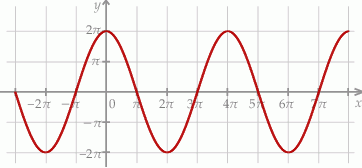
Na rysunku przedstawiono fragment wykresu pewnej funkcji 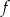 określonej dla każdej liczby rzeczywistej
określonej dla każdej liczby rzeczywistej  . Jeden z podanych poniżej wzorów jest wzorem tej funkcji. Wskaż wzór funkcji
. Jeden z podanych poniżej wzorów jest wzorem tej funkcji. Wskaż wzór funkcji 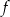 .
.
A) 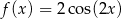 B)
B) 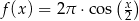
C) 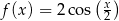 D)
D) 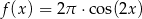
Wielomian 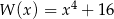 jest podzielny przez
jest podzielny przez
A) 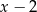 B)
B) 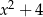 C)
C) 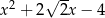 D)
D) 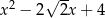
Zadania otwarte
Rozwiąż równanie 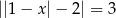 .
.
Oblicz granicę 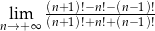 .
.
Udowodnij, że jeżeli 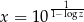 i
i 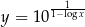 , to
, to 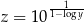 .
.
Rzucono kostką do gry trzy razy. Za pierwszym razem nie wyrzucono 4 oczek. Oblicz prawdopodobieństwo, że suma oczek w trzech rzutach jest równa 15.
Rozwiąż nierówność, której lewa strona jest sumą szeregu geometrycznego
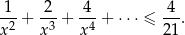
Długości wysokości trójkąta o bokach 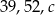 , gdzie
, gdzie 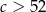 tworzą ciąg arytmetyczny. Oblicz promień okręgu wpisanego w ten trójkąt.
tworzą ciąg arytmetyczny. Oblicz promień okręgu wpisanego w ten trójkąt.
Rozwiąż równanie 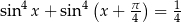 w przedziale
w przedziale 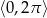 .
.
Wyznacz wszystkie wartości parametru 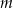 , dla których trójmian kwadratowy
, dla których trójmian kwadratowy
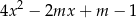
ma dwa różne pierwiastki rzeczywiste 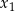 oraz
oraz 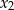 , spełniające warunki:
, spełniające warunki:
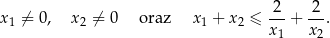
Dana jest funkcja 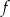 określona wzorem
określona wzorem 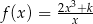 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej 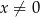 . Oblicz wartość
. Oblicz wartość 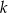 , dla której prosta o równaniu
, dla której prosta o równaniu 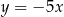 jest styczna do wykresu funkcji
jest styczna do wykresu funkcji 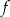 .
.
W okrąg o środku 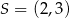 wpisano trapez w taki sposób, że jedna podstawa jest średnicą okręgu, a druga jest zawarta w prostej o równaniu
wpisano trapez w taki sposób, że jedna podstawa jest średnicą okręgu, a druga jest zawarta w prostej o równaniu 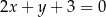 . Pole tego trapezu jest równe
. Pole tego trapezu jest równe 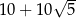 . Oblicz współrzędne tych wierzchołków trapezu, które są końcami jego krótszej podstawy.
. Oblicz współrzędne tych wierzchołków trapezu, które są końcami jego krótszej podstawy.
Z kawałka blachy w kształcie sześciokąta foremnego o boku długości 60 cm robimy pudełko o sześciokątnym dnie (otwarte od góry) w następujący sposób: przy każdym wierzchołku odcinamy taki sam deltoid, tnąc w tej samej odległości od wierzchołka raz prostopadle do jednego, a drugi raz do drugiego boku, następnie zaginamy blachę wzdłuż przerywanych linii i lutujemy krawędzie (zobacz rysunek).
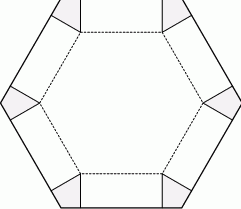
Oblicz długość krawędzi podstawy tego pudełka, którego objętość jest największa. Oblicz tę objętość.

