/Szkoła podstawowa/Egzamin ósmoklasisty/Egzamin 2022/Próbne testy
Próbny Egzamin Ósmoklasisty
z Matematyki Zestaw przygotowany przez serwis zadania.info 21 maja 2022 Czas pracy: 100 minut
W ramach prac konserwacyjnych opróżniono z wody zbiornik retencyjny. Wykres przedstawia zależność ilości pozostałej w zbiorniku wody (w 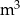 ) od czasu pracy pomp (w godzinach).
) od czasu pracy pomp (w godzinach).
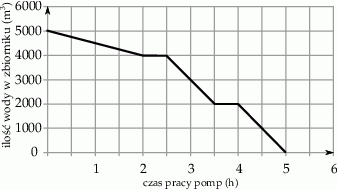
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Po 3,5 h wypompowano ze zbiornika połowę wody. | P | F |
Po 1 h wypompowano ze zbiornika 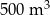 wody. wody. | P | F |
Korzystając z tego, że 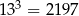 i
i 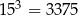 , oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
, oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
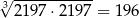 | P | F |
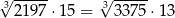 | P | F |
Ile spośród liczb: 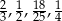 spełnia warunek
spełnia warunek 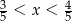 ?
?
Wybierz odpowiedź spośród podanych.
A) Jedna liczba. B) Dwie liczby. C) Trzy liczby. D) Cztery liczby.
Dane są liczby: 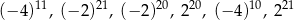 .
.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Wśród podanych liczb jest więcej liczb dodatnich, niż ujemnych. | P | F |
Wśród podanych liczb są 3 liczby równe 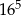 . . | P | F |
W pewnej hurtowni za 120 jednakowych długopisów i 360 jednakowych ołówków zapłacono 600 zł. Jaka byłaby cena zakupu 170 takich samych długopisów i 510 takich samych ołówków w tej hurtowni? Wybierz odpowiedź spośród podanych.
A) 850 zł B) 800 zł C) 780 zł D) 680 zł
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Liczba 16848 jest liczbą podzielną przez 32. | P | F |
| Liczba 16848 jest wielokrotnością 81. | P | F |
Dane są liczby  i
i 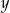 spełniające warunki:
spełniające warunki: 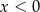 i
i 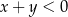 . Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Liczba 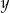 musi być ujemna. musi być ujemna. | P | F |
Liczby  i i 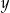 mogą być równe. mogą być równe. | P | F |
Pan Kazimierz chce kupić 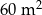 papy. Papa jest sprzedawana w rolkach o szerokości 1 m. Pan Kazimierz pod uwagę wziął dwa rodzaje papy.
papy. Papa jest sprzedawana w rolkach o szerokości 1 m. Pan Kazimierz pod uwagę wziął dwa rodzaje papy.
| Typ papy | Długość papy w rolce | Cena papy |
| I rodzaj | 15 m | 75 zł za 1 rolkę |
| II rodzaj | 3 m | 6 zł za 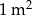 |
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Cena 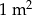 papy I rodzaju jest niższa niż cena papy I rodzaju jest niższa niż cena 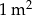 papy II rodzaju. papy II rodzaju. | P | F |
| Kupując tańszą papę, pan Kazimierz zaoszczędzi 40 zł. | P | F |
Informacja do zadań 9 i 10
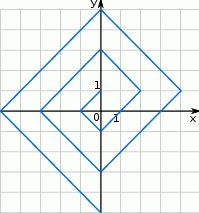
Zaczynając od punktu 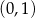 budujemy łamaną, której część składającą się z 10 odcinków przedstawiono na rysunku. Kolejne odcinki łamanej numerujemy kolejnymi liczbami naturalnymi. Pierwszy odcinek łamanej ma długość
budujemy łamaną, której część składającą się z 10 odcinków przedstawiono na rysunku. Kolejne odcinki łamanej numerujemy kolejnymi liczbami naturalnymi. Pierwszy odcinek łamanej ma długość 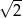 .
.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Jeżeli  jest liczbą parzystą, to odcinek o numerze jest liczbą parzystą, to odcinek o numerze  jest równoległydo odcinka o numerze 3. jest równoległydo odcinka o numerze 3. | P | F |
Jeżeli  jest liczbą nieparzystą, to długość odcinka o numerze jest liczbą nieparzystą, to długość odcinka o numerze  jest równa jest równa 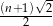 . . | P | F |
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Łamana złożona z 8 początkowych odcinków ma długość 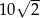 . . | P | F |
Długość setnego odcinka jest równa 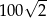 . . | P | F |
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Emil kolekcjonuje modele samochodów. Co trzeci z jego modeli to model samochodu terenowego, co czwarty to model ciężarówki, a pozostałe 20 modeli to modele samochodów osobowych. Emil ma w swojej kolekcji
A) 64 modele. B) 48 modeli. C) 36 modeli. D) 32 modele.
W pudełku jest 30 kul białych i 20 czarnych. Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Jeżeli 10 kul białych zostanie zastąpionych kulami czarnymi, to prawdopodobieństwa wylosowania kuli czarnej i białej będą równe. | P | F |
| Jeżeli podwoimy liczbę kul czarnych w pudełku, to prawdopodobieństwo wylosowania kuli czarnej wzrośnie dwukrotnie. | P | F |
Dany jest trapez równoramienny 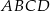 o podstawach długości 10 cm, 6 cm i ramieniu długości
o podstawach długości 10 cm, 6 cm i ramieniu długości 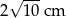 . Odcinek
. Odcinek 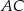 jest przekątną tego trapezu.
jest przekątną tego trapezu.
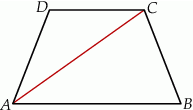
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Trójkąt 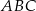 jest równoramienny. jest równoramienny. | P | F |
| Wysokość trapezu ma długość 5 cm. | P | F |
Który z poniższych rysunków nie może być siatką graniastosłupa prawidłowego trójkątnego? Wybierz odpowiedź spośród podanych.
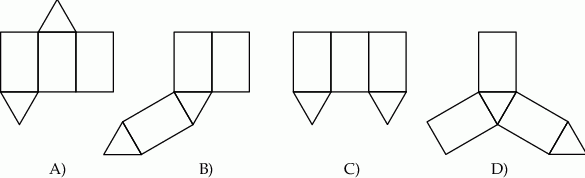
W prostopadłościennym akwarium, o wymiarach podanych na rysunku, woda sięga 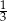 jego wysokości.
jego wysokości.
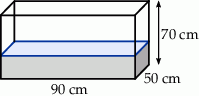
Ile litrów wody jest w akwarium?
Wybierz odpowiedź spośród podanych.
A) 105000 litrów B) 105 litrów C) 1050 litrów D) 10500 litrów
Jacek miał wziąć udział w obozie narciarskim, ale zachorował i zamiast niego na obóz pojechał jego dwa razy starszy brat. Ta zamiana spowodowała, że średnia wieku uczestników obozu wzrosła o rok. Oblicz, ile lat ma Jacek, jeżeli w obozie wzięło udział 12 osób. Zapisz obliczenia.
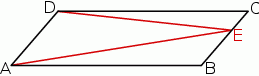
Na rysunku przedstawiono równoległobok 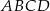 i trójkąt
i trójkąt 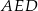 . Punkt
. Punkt 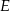 leży na odcinku
leży na odcinku 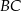 . Uzasadnij, że pole równoległoboku
. Uzasadnij, że pole równoległoboku 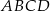 jest dwa razy większe od pola trójkąta
jest dwa razy większe od pola trójkąta 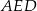 .
.
W pewnej klasie liczba chłopców stanowi 75% liczby dziewcząt. Gdyby do tej klasy doszło jeszcze czterech chłopców, to liczba chłopców byłaby równa liczbie dziewcząt. Ile dziewcząt jest w tej klasie? Zapisz obliczenia.
Pole powierzchni całkowitej graniastosłupa prawidłowego czworokątnego jest równe 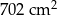 . Pole podstawy tej bryły stanowi 60% pola powierzchni jednej ściany bocznej. Oblicz wysokość bryły. Zapisz obliczenia.
. Pole podstawy tej bryły stanowi 60% pola powierzchni jednej ściany bocznej. Oblicz wysokość bryły. Zapisz obliczenia.

