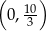Zadanie nr 7922647
Wyznacz punkt wspólny symetralnej odcinka 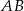 , gdzie
, gdzie 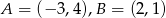 , oraz osi
, oraz osi 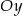 .
.
Rozwiązanie
Zaczynamy od rysunku
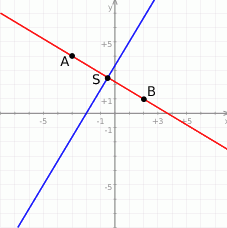
Sposób I
Pamiętamy, że symetralna odcinka jest to taka prosta która jest równo oddalona od końców tego odcinka. Otrzymujemy więc równanie
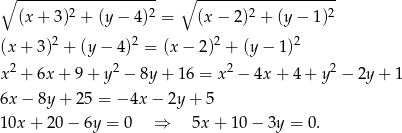
Żeby policzyć punkt przecięcia z osią 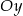 wystarczy podstawić
wystarczy podstawić 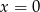
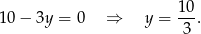
Zatem punkt przecięcia ma współrzędne 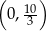 .
.
Sposób II
Wyznaczamy środek odcinka 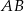
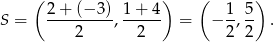
Skorzystamy ze wzoru
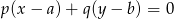
na równanie prostej prostopadłej do wektora 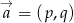 i przechodzącej przez punkt
i przechodzącej przez punkt 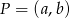 . W naszym przypadku punktem
. W naszym przypadku punktem 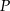 będzie środek
będzie środek 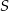 odcinka
odcinka 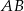 (symetralna odcinka zawsze przechodzi przez jego środek) natomiast wektor będzie równy
(symetralna odcinka zawsze przechodzi przez jego środek) natomiast wektor będzie równy
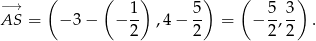
Symetralna ma więc równanie
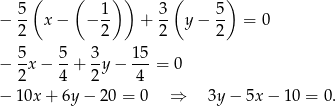
Znowu podstawiamy 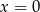 i otrzymujemy
i otrzymujemy
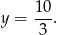
Zatem współrzędne punktu przecięcia to 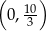 .
.
Sposób III
Oznaczmy przez 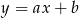 równanie szukanej symetralnej. Wyznaczamy równanie prostej przechodzącej przez punkty
równanie szukanej symetralnej. Wyznaczamy równanie prostej przechodzącej przez punkty 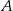 i
i 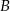 . Otrzymujemy układ równań
. Otrzymujemy układ równań
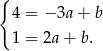
Odejmujemy stronami i otrzymujemy
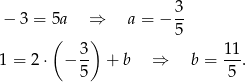
Wyznaczamy współrzędne środka odcinka 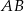
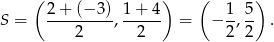
Napiszemy teraz równanie prostej prostopadłej do prostej 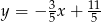 i przechodzącej przez punkt
i przechodzącej przez punkt 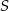 . Zaczynamy od wyznaczenia współczynnika kierunkowego z warunku na prostopadłość
. Zaczynamy od wyznaczenia współczynnika kierunkowego z warunku na prostopadłość
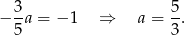
Teraz podstawiamy współrzędne punktu  i obliczamy
i obliczamy 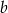
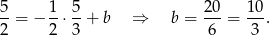
Zatem otrzymujemy równanie prostej 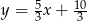 . Teraz wystarczy podstawić tylko
. Teraz wystarczy podstawić tylko 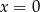
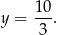
Czyli punkt przecięcia ma współrzędne 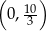 .
.
Odpowiedź: