/Szkoła średnia/Zadania maturalne/Matura 2023
Egzamin Maturalny
z Matematyki poziom rozszerzony 12 maja 2023 Czas pracy: 180 minut
W chwili początkowej 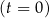 masa substancji jest równa 4 gramom. Wskutek rozpadu cząsteczek tej substancji jej masa się zmniejsza. Po każdej kolejnej dobie ubywa 19% masy, jaka była na koniec doby poprzedniej. Dla każdej liczby całkowitej
masa substancji jest równa 4 gramom. Wskutek rozpadu cząsteczek tej substancji jej masa się zmniejsza. Po każdej kolejnej dobie ubywa 19% masy, jaka była na koniec doby poprzedniej. Dla każdej liczby całkowitej 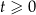 funkcja
funkcja 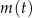 określa masę substancji w gramach po
określa masę substancji w gramach po 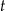 pełnych dobach (czas liczymy od chwili początkowej). Wyznacz wzór funkcji
pełnych dobach (czas liczymy od chwili początkowej). Wyznacz wzór funkcji 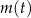 . Oblicz, po ilu pełnych dobach masa tej substancji będzie po raz pierwszy mniejsza od 1,5 grama.
. Oblicz, po ilu pełnych dobach masa tej substancji będzie po raz pierwszy mniejsza od 1,5 grama.
Tomek i Romek postanowili rozegrać między sobą pięć partii szachów. Prawdopodobieństwo wygrania pojedynczej partii przez Tomka jest równe  . Oblicz prawdopodobieństwo wygrania przez Tomka co najmniej czterech z pięciu partii. Wynik podaj w postaci ułamka zwykłego nieskracalnego.
. Oblicz prawdopodobieństwo wygrania przez Tomka co najmniej czterech z pięciu partii. Wynik podaj w postaci ułamka zwykłego nieskracalnego.
Funkcja 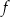 jest określona wzorem
jest określona wzorem 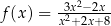 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Punkt
. Punkt 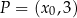 należy do wykresu funkcji
należy do wykresu funkcji 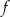 . Oblicz
. Oblicz 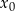 oraz wyznacz równanie stycznej do wykresu funkcji
oraz wyznacz równanie stycznej do wykresu funkcji 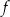 w punkcie
w punkcie 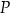 .
.
Liczby rzeczywiste  oraz
oraz 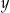 spełniają jednocześnie równanie
spełniają jednocześnie równanie 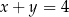 i nierówność
i nierówność
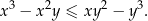
Wykaż, że 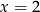 oraz
oraz 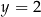 .
.
Dany jest trójkąt prostokątny 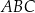 , w którym
, w którym 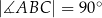 oraz
oraz 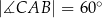 . Punkty
. Punkty 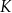 i
i 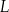 leżą na bokach – odpowiednio –
leżą na bokach – odpowiednio – 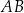 i
i 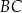 tak, że
tak, że 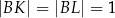 (zobacz rysunek). Odcinek
(zobacz rysunek). Odcinek 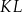 przecina wysokość
przecina wysokość 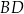 tego trójkąta w punkcie
tego trójkąta w punkcie 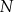 , a ponadto
, a ponadto 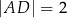 .
.
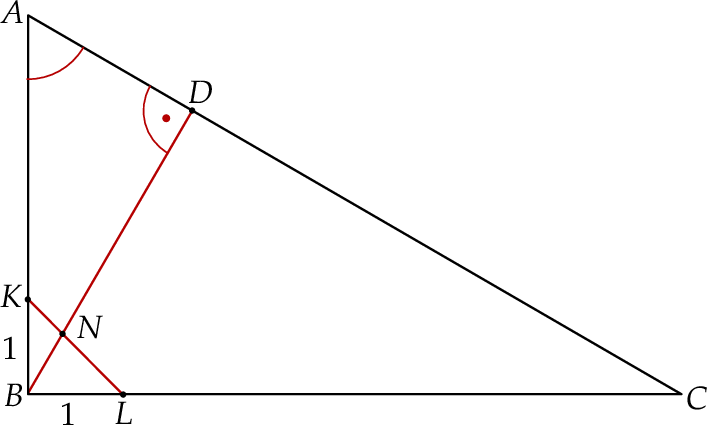
Wykaż, że 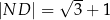 .
.
Rozwiąż równanie 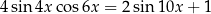 .
.
Dany jest sześcian 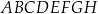 o krawędzi długości 6. Punkt
o krawędzi długości 6. Punkt 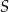 jest punktem przecięcia przekątnych
jest punktem przecięcia przekątnych 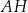 i
i 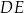 ściany bocznej
ściany bocznej 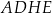 (zobacz rysunek).
(zobacz rysunek).
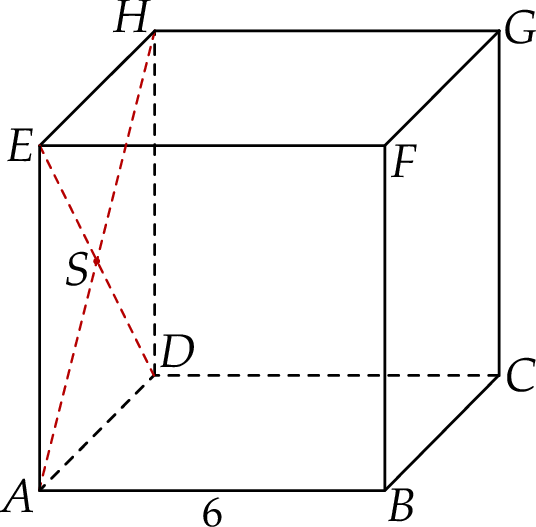
Oblicz wysokość trójkąta 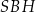 poprowadzoną z punktu
poprowadzoną z punktu 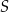 na bok
na bok 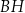 tego trójkąta.
tego trójkąta.
Czworokąt 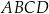 , w którym
, w którym 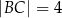 i
i 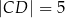 , jest opisany na okręgu. Przekątna
, jest opisany na okręgu. Przekątna 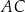 tego czworokąta tworzy z bokiem
tego czworokąta tworzy z bokiem 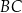 kąt o mierze
kąt o mierze 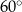 , natomiast z bokiem
, natomiast z bokiem 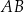 – kąt ostry, którego sinus jest równy
– kąt ostry, którego sinus jest równy 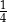 . Oblicz obwód czworokąta
. Oblicz obwód czworokąta 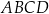 .
.
Rozwiąż nierówność 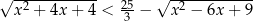 .
.
Określamy kwadraty 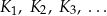 następująco:
następująco:
-
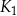 jest kwadratem o boku długości
jest kwadratem o boku długości 
-
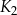 jest kwadratem, którego każdy wierzchołek leży na innym boku kwadratu
jest kwadratem, którego każdy wierzchołek leży na innym boku kwadratu 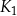 i dzieli ten bok w stosunku 1 : 3
i dzieli ten bok w stosunku 1 : 3 -
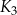 jest kwadratem, którego każdy wierzchołek leży na innym boku kwadratu
jest kwadratem, którego każdy wierzchołek leży na innym boku kwadratu 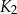 i dzieli ten bok w stosunku 1 : 3
i dzieli ten bok w stosunku 1 : 3
i ogólnie, dla każdej liczby naturalnej 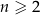 ,
,
-
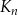 jest kwadratem, którego każdy wierzchołek leży na innym boku kwadratu
jest kwadratem, którego każdy wierzchołek leży na innym boku kwadratu 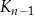 i dzieli ten bok w stosunku 1 : 3.
i dzieli ten bok w stosunku 1 : 3.
Obwody wszystkich kwadratów określonych powyżej tworzą nieskończony ciąg geometryczny. Na rysunku przedstawiono kwadraty utworzone w sposób opisany powyżej.
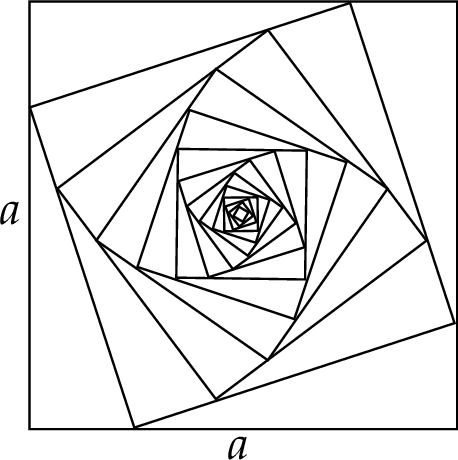
Oblicz sumę wszystkich wyrazów tego nieskończonego ciągu.
Wyznacz wszystkie wartości parametru 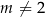 , dla których równanie
, dla których równanie
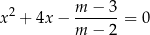
ma dwa różne rozwiązania rzeczywiste 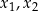 spełniające warunek
spełniające warunek 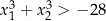 .
.
Funkcja 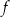 jest określona wzorem
jest określona wzorem
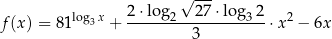
dla każdej liczby dodatniej  .
.
-
Wykaż, że dla każdej liczby dodatniej
 wzór funkcji
wzór funkcji 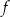 można równoważnie przekształcić do postaci
można równoważnie przekształcić do postaci 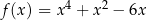 .
. -
Oblicz najmniejszą wartość funkcji
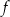 określonej dla każdej liczby dodatniej
określonej dla każdej liczby dodatniej  .
.
W kartezjańskim układzie współrzędnych 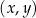 prosta
prosta 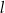 o równaniu
o równaniu 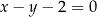 przecina parabolę o równaniu
przecina parabolę o równaniu 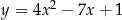 w punktach
w punktach 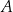 oraz
oraz 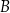 . Odcinek
. Odcinek 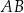 jest średnicą okręgu
jest średnicą okręgu 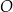 . Punkt
. Punkt 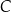 leży na okręgu
leży na okręgu 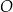 nad prostą
nad prostą 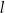 , a kąt
, a kąt 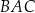 jest ostry i ma miarę
jest ostry i ma miarę  taką, że
taką, że 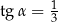 (zobacz rysunek).
(zobacz rysunek).
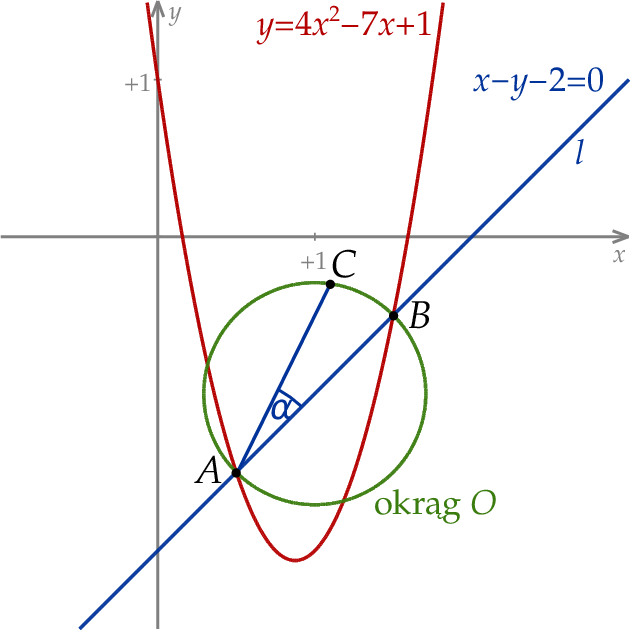
Oblicz współrzędne punktu 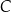 .
.

