/Szkoła średnia/Zadania maturalne/Matura 2023

Optymalizacja – geometria analityczna poziom rozszerzony

Zadanie 1

Dana jest parabola opisana równaniem 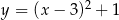2 y = (x− 3) + 1 . Tworzymy trójkąty 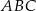ABC takie, że punkt 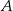A leży w początku układu współrzędnych, punkt 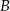B o współrzędnych 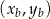(xb ,yb ) leży na paraboli, punkt 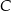C ma współrzędne (xb,0) .

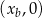  • Napisz wzór funkcji 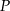P , określającej pole trójkąta 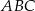ABC w zależności od 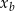xb dla xb > 0 .
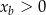  • Znajdź trójkąt o największym polu dla xb ∈ [0;2] ; w odpowiedzi podaj współrzędne punktu C .

Zadanie 2

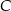Który z odcinków łączących dowolny punkt paraboli o równaniu 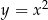y = x2 z punktem 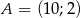A = (10 ;2 ) ma najmniejszy kwadrat długości?

Zadanie 3

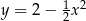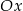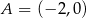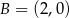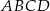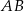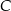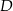Parabola o równaniu 1 2 y = 2 − 2x przecina oś Ox układu współrzędnych w punktach A = (− 2,0) i B = (2,0) . Rozpatrujemy wszystkie trapezy równoramienne ABCD , których dłuższą podstawą jest odcinek AB , a końce C i D krótszej podstawy leżą na paraboli (zobacz rysunek).

PIC

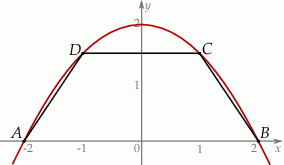
Wyznacz pole trapezu 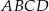ABCD w zależności od pierwszej współrzędnej wierzchołka 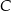C . Oblicz współrzędne wierzchołka 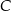C tego z rozpatrywanych trapezów, którego pole jest największe.

Zadanie 4

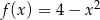Dwa wierzchołki prostokąta leżą na osi x , a pozostałe dwa należą do paraboli o równaniu f(x) = 4 − x 2 i znajdują się powyżej osi x .

  • Podaj wzór funkcji opisującej pole tego prostokąta w zależności od jego podstawy.
  • Dla jakiej długości podstawy pole tego prostokąta jest równe 6.
  • Dla jakiej długości podstawy pole tego prostokąta jest największe?

Zadanie 5

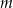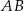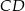Wyznacz wartość parametru m , dla której pole koła stycznego do prostych zawierających boki AB i CD równoległoboku 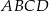ABCD o wierzchołkach 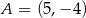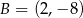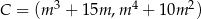A = (5,− 4) , B = (2,− 8) , C = (m 3 + 15m ,m 4 + 10m 2) jest najmniejsze możliwe. Oblicz to pole.

Zadanie 6

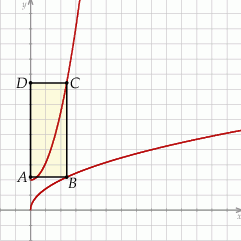
Rozpatrujemy prostokąty 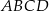ABCD , których dwa wierzchołki leżą na osi 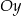Oy , jeden wierzchołek leży na paraboli określonej równaniem 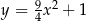y = 9x2 + 1 4 , jeden wierzchołek leży na wykresie funkcji 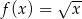f(x ) = √x-- określonej dla 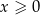x ≥ 0 . Oblicz pole tego z tych prostokątów, który ma najmniejszy możliwy obwód.

PIC

Zadanie 7

Na wykresie funkcji 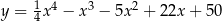1 4 3 2 y = 4x − x − 5x + 22x + 50 znajdź współrzędne punktu 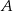A , którego odległość od prostej o równaniu 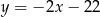y = − 2x − 2 2 jest najmniejsza.

Wersja PDF
Rozwiązania