/Szkoła średnia/Zadania maturalne/Matura 2023
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis zadania.info poziom podstawowy 25 marca 2023
Dany jest układ równań
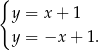
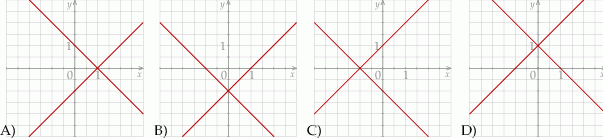
Na którym z rysunków przedstawiona jest interpretacja geometryczna tego układu równań?
Liczba 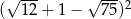 jest równa
jest równa
A) 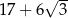 B)
B) 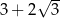 C)
C) 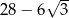 D)
D) 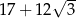
Pani Łucja kupiła obligacje Skarbu Państwa za 20 000 zł oprocentowane 6% w skali roku. Odsetki są naliczane i kapitalizowane co rok. Wartość obligacji kupionych przez panią Łucję będzie po dwóch latach równa
A) 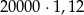 B)
B) 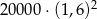 C)
C) 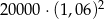 D)
D) 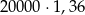
Liczba dwukrotnie mniejsza od 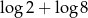 jest równa
jest równa
A) 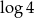 B)
B) 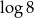 C)
C) 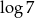 D)
D) 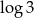
Dla każdej liczby rzeczywistej  wartość wyrażenia
wartość wyrażenia 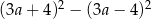 jest równa
jest równa
A) 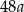 B) 0 C)
B) 0 C) 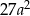 D)
D) 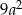
Wszystkich liczb naturalnych czterocyfrowych parzystych, w których cyfra 5 występuje dokładnie jeden raz, jest
A) 3285 B) 1125 C) 765 D) 3240
Informacja do zadań 7.1 i 7.2
Na rysunku, w kartezjańskim układzie współrzędnych 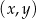 , przedstawiono wykres funkcji
, przedstawiono wykres funkcji 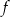 określonej dla każdego
określonej dla każdego ![x ∈ (− 4,5]](https://img.zadania.info/zes/0089475/HzesT23x.gif) . Na tym wykresie zaznaczono punkty o współrzędnych całkowitych.
. Na tym wykresie zaznaczono punkty o współrzędnych całkowitych.
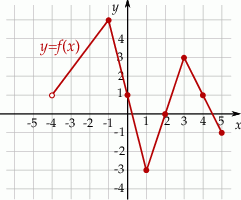
Wyznacz zbiór wartości funkcji 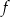 .
.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Dla każdego argumentu z przedziału 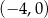 funkcja funkcja 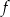 przyjmuje wartości dodatnie. przyjmuje wartości dodatnie. | P | F |
Funkcja 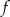 ma cztery miejsca zerowe. ma cztery miejsca zerowe. | P | F |
Wykaż, że jeśli  jest liczbą nieparzystą, to liczba
jest liczbą nieparzystą, to liczba 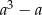 jest podzielna przez 12.
jest podzielna przez 12.
Dodatnie liczby  i
i 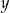 spełniają warunek
spełniają warunek 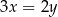 . Wynika stąd, że wartość wyrażenia
. Wynika stąd, że wartość wyrażenia 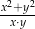 jest równa
jest równa
A)  B)
B) 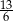 C)
C) 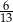 D)
D) 
Dana jest funkcja liniowa 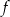 określona wzorem
określona wzorem 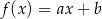 , gdzie
, gdzie  i
i 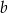 są liczbami rzeczywistymi. Rozwiązaniem nierówności
są liczbami rzeczywistymi. Rozwiązaniem nierówności 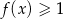 jest przedział
jest przedział ![(− ∞ ,3]](https://img.zadania.info/zes/0089475/HzesT44x.gif) . Współczynniki
. Współczynniki  i
i 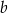 we wzorze funkcji
we wzorze funkcji 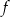 spełniają warunki
spełniają warunki
A) 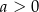 i
i 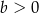 B)
B) 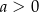 i
i 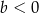 C)
C) 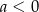 i
i 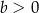 D)
D) 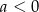 i
i 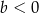
Dana jest funkcja wykładnicza 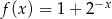 określona dla
określona dla 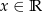 .
.
Dokończ zdanie tak, aby było prawdziwe. Wybierz odpowiedź A albo B oraz jej uzasadnienie 1, 2 albo 3.
Zbiorem wartości funkcji 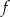 jest przedział
jest przedział
A) 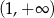 , , | B) 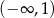 , , |
ponieważ wykres funkcji 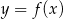 można otrzymać z wykresu funkcji
można otrzymać z wykresu funkcji 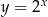 poprzez
poprzez
| 1) | symetrię względem osi 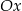 i przesunięcie o 1 jednostkę w dół. i przesunięcie o 1 jednostkę w dół. |
| 2) | symetrię względem osi 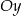 i przesunięcie o 1 jednostkę w górę. i przesunięcie o 1 jednostkę w górę. |
| 3) | symetrię względem osi 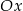 i przesunięcie o 1 jednostkę w górę. i przesunięcie o 1 jednostkę w górę. |
Przybliżenie liczby 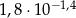 jest równe 0,07165929. Przybliżeniem liczby
jest równe 0,07165929. Przybliżeniem liczby 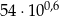 z dokładnością do 3 miejsca po przecinku jest liczba
z dokładnością do 3 miejsca po przecinku jest liczba
A) 21,499 B) 214,978 C) 2149,779 D) 71,659
W ciągu arytmetycznym 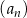 , określonym dla
, określonym dla 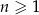 , spełniony jest warunek
, spełniony jest warunek 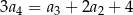 . Różnica
. Różnica  tego ciągu jest równa
tego ciągu jest równa
A) 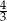 B) 1 C)
B) 1 C)  D)
D) 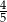
Rozwiąż równanie 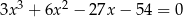 .
.
Dany jest trójkąt 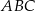 , w którym
, w którym 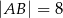 ,
, 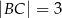 ,
, 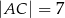 . Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Cosinus kąta 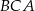 jest równy jest równy 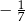 . . | P | F |
Trójkąt 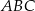 jest ostrokątny. jest ostrokątny. | P | F |
Liczba 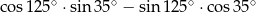 jest równa
jest równa
A) 1 B) 0 C) 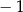 D)
D) 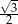
Dany jest ciąg geometryczny 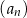 , określony dla każdej liczby naturalnej
, określony dla każdej liczby naturalnej 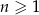 . W tym ciągu
. W tym ciągu 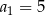 ,
, 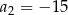 ,
, 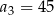 .
.
Dokończ zdanie. Wybierz dwie właściwe odpowiedzi spośród podanych.
Wzór ogólny ciągu 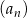 ma postać
ma postać
A) 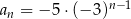 B)
B) 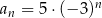
C) 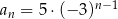 D)
D) 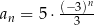
E) 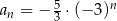 F)
F) 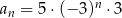
Dany jest ciąg 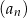 określony wzorem
określony wzorem 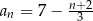 dla każdej liczby naturalnej
dla każdej liczby naturalnej 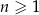 . Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Ciąg 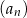 jest geometryczny. jest geometryczny. | P | F |
Suma szesnastu początkowych wyrazów ciągu 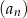 jest równa 56. jest równa 56. | P | F |
Promień okręgu danego równaniem 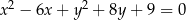 ma długość
ma długość
A) 2 B) 4 C) 9 D) 16
Do wyznaczenia trzech pastwisk na pewnej łące należy użyć ogrodzenia elektrycznego o łącznej długości 960 metrów. Dwa z tych pastwisk mają mieć kwadratowy kształt, a trzecie ma mieć kształt prostokąta, którego jeden z boków jest dwa razy dłuższy od boku pastwiska w kształcie kwadratu (zobacz rysunek).
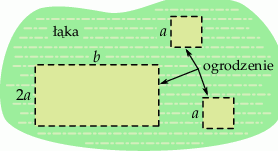
Oblicz wymiary  i
i 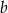 tych pastwisk tak, aby ich łączna powierzchnia była największa możliwa. Oblicz tą największą powierzchnię.
tych pastwisk tak, aby ich łączna powierzchnia była największa możliwa. Oblicz tą największą powierzchnię.
Informacja do zadań 21.1 – 21.3
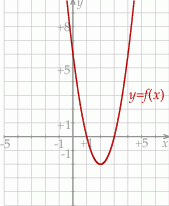
Dana jest funkcja kwadratowa 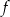 , której fragment wykresu przedstawiono na rysunku poniżej. Wierzchołek paraboli, która jest wykresem funkcji
, której fragment wykresu przedstawiono na rysunku poniżej. Wierzchołek paraboli, która jest wykresem funkcji 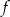 , oraz punkty przecięcia paraboli z osiami układu współrzędnych mają współrzędne całkowite.
, oraz punkty przecięcia paraboli z osiami układu współrzędnych mają współrzędne całkowite.
Funkcja 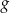 jest określona za pomocą funkcji
jest określona za pomocą funkcji 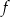 następująco:
następująco: 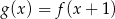 . Wykres funkcji
. Wykres funkcji 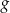 przedstawiono na rysunku
przedstawiono na rysunku
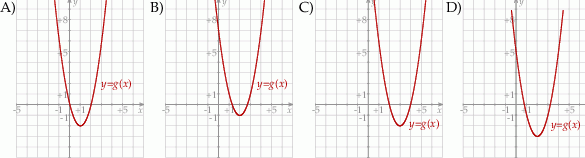
Wyznacz wzór funkcji kwadratowej 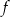 w postaci kanonicznej.
w postaci kanonicznej.
Rozwiąż nierówność 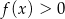 .
.
W pudełku są tylko kule białe, czarne i zielone. Kul białych jest dwa razy więcej niż czarnych, a czarnych jest trzy razy więcej niż zielonych. Z pudełka losujemy jedną kulę. Prawdopodobieństwo wylosowania kuli czarnej lub białej jest równe
A)  B)
B) 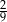 C)
C) 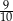 D)
D) 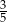
W trójkącie prostokątnym o przyprostokątnych długości 5 i 12 połączono wierzchołek 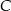 kąta prostego ze środkiem
kąta prostego ze środkiem 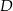 przeciwprostokątnej. Długość odcinka
przeciwprostokątnej. Długość odcinka 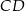 jest równa
jest równa
A) 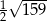 B) 6,5 C) 13 D)
B) 6,5 C) 13 D) 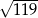
Odcinki 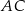 i
i 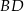 przecinają się w punkcie
przecinają się w punkcie 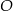 . Ponadto
. Ponadto 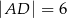 ,
, 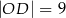 i
i 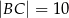 . Kąty
. Kąty 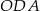 i
i 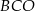 są proste (zobacz rysunek).
są proste (zobacz rysunek).
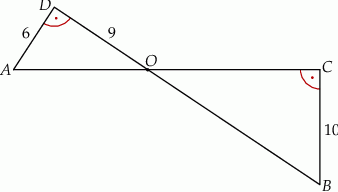
Długość odcinka 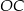 jest równa
jest równa
A) 12 B) 15 C) 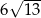 D)
D) 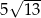
Informacja do zadań 25.1 i 25.2
Na płaszczyźnie, w kartezjańskim układzie współrzędnych 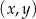 , dane są proste
, dane są proste 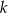 oraz
oraz 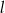 o równaniach
o równaniach
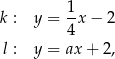
gdzie  jest pewną liczbą rzeczywistą.
jest pewną liczbą rzeczywistą.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Proste 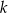 i i 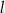 mogą mięc nieskończenie wiele punktów wspólnych. mogą mięc nieskończenie wiele punktów wspólnych. | P | F |
Punkt wspólny prostych 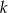 i i 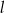 może leżeć w I ćwiartce układu współrzędnych może leżeć w I ćwiartce układu współrzędnych | P | F |
Proste 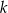 i
i 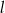 są prostopadłe. Wyznacz ich punkt przecięcia.
są prostopadłe. Wyznacz ich punkt przecięcia.
Rozwiązaniem równania 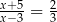 jest liczba
jest liczba
A) 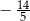 B)
B) 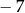 C)
C) 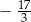 D)
D) 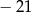
W ostrosłupie prawidłowym czworokątnym 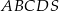 wszystkie krawędzie mają jednakową długość.
wszystkie krawędzie mają jednakową długość.
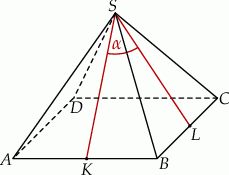
Oblicz cosinus kąta utworzonego przez wysokości 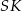 i
i 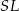 dwóch sąsiednich ścian bocznych.
dwóch sąsiednich ścian bocznych.
Przeprowadzono badanie dziennej liczby pokonywanych kilometrów przez kierowców pięciu taksówek. Na koniec dnia otrzymano następujące wyniki:
– I kierowca – 169 kilometrów
– II kierowca – 190 kilometrów
– III kierowca – 183 kilometrów
– IV kierowca – 197 kilometrów
– V kierowca – 211 kilometrów.
Odchylenie standardowe liczby przejechanych kilometrów jest równe 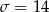 . Podaj numery kierowców, dla których liczba przejechanych kilometrów mieści się w przedziale określonym przez jedno odchylenie standardowe od średniej.
. Podaj numery kierowców, dla których liczba przejechanych kilometrów mieści się w przedziale określonym przez jedno odchylenie standardowe od średniej.
Powierzchnię boczną graniastosłupa prawidłowego trójkątnego rozcięto wzdłuż krawędzi bocznej graniastosłupa i rozłożono na płaszczyźnie. Otrzymano w ten sposób prostokąt 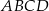 , w którym bok
, w którym bok 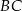 odpowiada krawędzi rozcięcia (wysokości graniastosłupa). Przekątna
odpowiada krawędzi rozcięcia (wysokości graniastosłupa). Przekątna 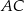 tego prostokąta ma długość 15 i tworzy z bokiem
tego prostokąta ma długość 15 i tworzy z bokiem 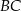 kąt o mierze
kąt o mierze 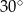 (zobacz rysunek).
(zobacz rysunek).
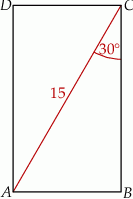
Długość krawędzi podstawy tego graniastosłupa jest równa.
A) 2,5 B) 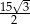 C)
C) 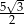 D) 7,5
D) 7,5
Informacja do zadań 30.1 i 30.2
Prosta przechodząca przez środek 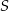 kwadratu
kwadratu 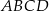 przecina proste zawierające jego boki
przecina proste zawierające jego boki 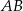 i
i 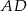 odpowiednio w punktach
odpowiednio w punktach 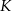 i
i 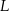 (zobacz rysunek).
(zobacz rysunek).
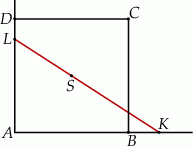
Jeżeli bok kwadratu ma długość 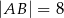 i
i 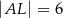 , to pole trójkąta
, to pole trójkąta 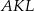 jest równe
jest równe
A) 32 B) 36 C) 40 D) 52
Wykaż, że