/Szkoła średnia/Zadania maturalne/Matura 2023
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis zadania.info poziom podstawowy 22 kwietnia 2023 Czas pracy: 180 minut
Liczba 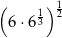 jest równa
jest równa
A) 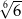 B)
B) 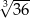 C)
C) 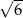 D)
D) 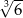
Pewną kwotę ulokowano w banku na lokacie kapitalizowanej raz w roku odsetkami w wysokości 6% zgromadzonego kapitału. Po sześciu latach oszczędzania w tym banku kwota zgromadzonego kapitału będzie większa od kwoty wpłaconej do banku o 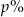 (z dokładnością do
(z dokładnością do 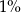 ). Zatem
). Zatem
A) 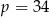 B)
B) 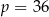 C)
C) 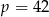 D)
D) 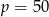
Wszystkich liczb naturalnych trzycyfrowych, w których zapisie dziesiętnym nie występuje cyfra 9, jest
A) 900 B) 648 C) 729 D) 512
Liczby rzeczywiste  i
i 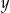 są dodatnie. Wyrażenie
są dodatnie. Wyrażenie 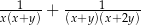 można przekształcić do postaci
można przekształcić do postaci
A) 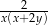 B)
B) 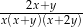 C)
C) 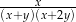 D)
D) 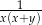
Na rysunku zaznaczono punkty wspólne dwóch równoległych prostych 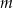 i
i  z prostymi
z prostymi 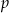 i
i 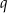 .
.
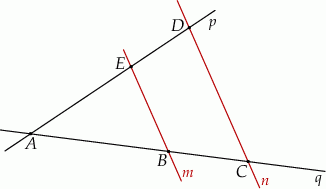
Dokończ zdanie. Wybierz dwie odpowiedzi, tak aby dla każdej z nich dokończenie poniższego zdania było prawdziwe.
Długości odcinków o końcach w punktach 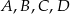 i
i 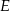 zawsze spełniają równość
zawsze spełniają równość
A) 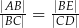 B)
B) 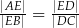 C)
C) 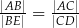
D) 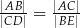 E)
E) 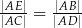 F)
F) 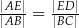
Funkcja 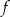 jest określona wzorem
jest określona wzorem 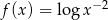 dla wszystkich liczb rzeczywistych dodatnich
dla wszystkich liczb rzeczywistych dodatnich  . Wartość funkcji
. Wartość funkcji 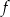 dla argumentu
dla argumentu 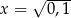 jest równa
jest równa
A) 1 B) 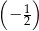 C)
C) 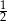 D)
D) 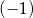
W rozwinięciu dziesiętnym ułamka  na trzydziestym miejscu po przecinku stoi cyfra
na trzydziestym miejscu po przecinku stoi cyfra
A) 7 B) 1 C) 2 D) 4
Dane są takie liczby całkowite  i
i 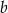 , że liczba
, że liczba 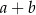 jest podzielna przez 5. Wykaż, że liczba
jest podzielna przez 5. Wykaż, że liczba 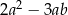 jest podzielna przez 5.
jest podzielna przez 5.
Wskaż nierówność, która opisuje przedział zaznaczony na osi liczbowej:
![]()
A) 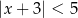 B)
B) 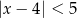 C)
C) 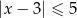 D)
D) 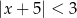
Klient banku wypłacił z bankomatu kwotę 1680 zł. Bankomat wydał kwotę w banknotach o nominałach 20 zł, 50 zł oraz 100 zł. Banknotów 100–złotowych było o 50% więcej niż 50–złotowych, a banknotów 20–złotowych było o 50% mniej niż 50–złotowych. Niech  oznacza liczbę banknotów 50–złotowych, a
oznacza liczbę banknotów 50–złotowych, a 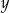 – liczbę banknotów 20–złotowych, które otrzymał ten klient. Poprawny układ równań prowadzący do obliczenia liczb
– liczbę banknotów 20–złotowych, które otrzymał ten klient. Poprawny układ równań prowadzący do obliczenia liczb  i
i 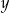 to
to
A) 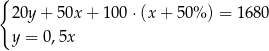 B)
B) 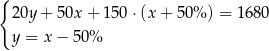
C) 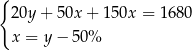 D)
D) 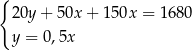
Informacja do zadań 11.1 i 11.2
W ciągu arytmetycznym 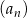 , określonym dla
, określonym dla 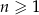 , wyraz szósty jest równy 3, a wyraz dziesiąty jest równy 15.
, wyraz szósty jest równy 3, a wyraz dziesiąty jest równy 15.
Jednym z wyrazów tego ciągu jest liczba
A) 2023 B) 1945 C) 1410 D) 2000
Oblicz dla jakich wartości  suma
suma  początkowych wyrazów ciągu
początkowych wyrazów ciągu 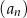 jest mniejsza od 729.
jest mniejsza od 729.
Dany jest kwadrat  o boku długości 8. Z wierzchołka
o boku długości 8. Z wierzchołka  zakreślono koło o promieniu równym długości boku kwadratu (zobacz rysunek).
zakreślono koło o promieniu równym długości boku kwadratu (zobacz rysunek).
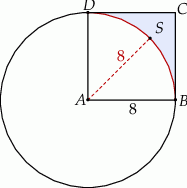
Oblicz pole powierzchni obszaru  otrzymanego z kwadratu
otrzymanego z kwadratu  przez wycięcie części pokrytej kołem.
przez wycięcie części pokrytej kołem.
Dana jest nierówność
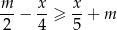
z parametrem 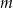 i niewiadomą
i niewiadomą  . Jeżeli liczba
. Jeżeli liczba 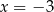 spełnia tą nierówność, to
spełnia tą nierówność, to
A) 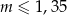 B)
B) 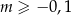 C)
C) 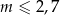 D)
D) 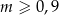
Jednym z rozwiązań równania 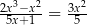 jest liczba
jest liczba
A) 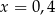 B)
B) 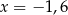 C)
C) 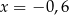 D)
D) 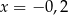
Krawędź boczna ostrosłupa prawidłowego czworokątnego ma długość 12 i jest nachylona do płaszczyzny podstawy pod kątem 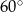 . Oblicz pole powierzchni całkowitej tego ostrosłupa.
. Oblicz pole powierzchni całkowitej tego ostrosłupa.
Iloczyn pierwiastków równania 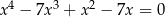 jest równy
jest równy
A) 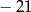 B) 14 C)
B) 14 C) 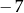 D) 0
D) 0
Dany jest ciąg 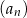 określony wzorem
określony wzorem 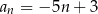 dla każdej liczby naturalnej
dla każdej liczby naturalnej 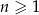 . Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Liczby 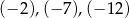 są trzema kolejnymi początkowymi wyrazami ciągu są trzema kolejnymi początkowymi wyrazami ciągu 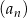 . . | P | F |
Ciąg 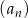 jest ciągiem arytmetycznym o różnicy równej 5. jest ciągiem arytmetycznym o różnicy równej 5. | P | F |
Największą liczbą naturalną, która spełnia nierówności 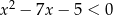 jest
jest
A) 0 B) 3 C) 7 D) 8
Punkt 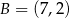 jest jednym z wierzchołków kwadratu
jest jednym z wierzchołków kwadratu 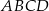 , a punkt
, a punkt 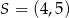 jest środkiem okręgu wpisanego w ten kwadrat. Przekątna tego kwadratu ma długość
jest środkiem okręgu wpisanego w ten kwadrat. Przekątna tego kwadratu ma długość
A) 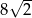 B)
B) 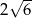 C)
C) 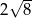 D)
D) 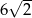
Dany jest trójkąt 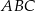 , w którym
, w którym 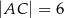 ,
, 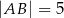 ,
, 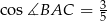 . Oblicz pole trójkąta
. Oblicz pole trójkąta 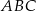 .
.
Średnicą okręgu jest odcinek 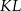 , gdzie
, gdzie 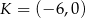 i
i 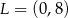 . Równanie tego okręgu ma postać
. Równanie tego okręgu ma postać
A) 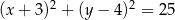 B)
B) 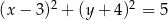
C) 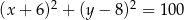 D)
D) 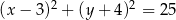
W romb o boku 2 i kącie 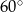 wpisano okrąg. Promień tego okręgu jest równy
wpisano okrąg. Promień tego okręgu jest równy
A) 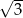 B)
B) 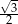 C)
C) 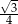 D)
D) 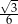
Punkty 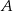 oraz
oraz  leżą na okręgu o środku
leżą na okręgu o środku 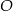 . Proste
. Proste 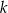 i
i 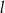 są styczne do tego okręgu w punktach – odpowiednio –
są styczne do tego okręgu w punktach – odpowiednio – 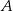 i
i 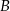 . Te proste przecinają się w punkcie
. Te proste przecinają się w punkcie 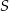 i tworzą kąt o mierze
i tworzą kąt o mierze 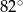 (zobacz rysunek).
(zobacz rysunek).
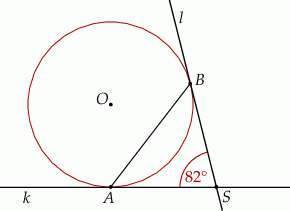
Miara kąta 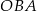 jest równa
jest równa
A) 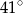 B)
B) 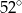 C)
C) 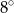 D)
D) 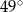
Dane są punkty 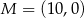 ,
, 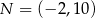 oraz
oraz 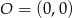 . Tangens kąta rozwartego
. Tangens kąta rozwartego 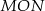 jest równy
jest równy
A) 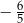 B)
B) 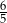 C) 1 D)
C) 1 D) 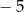
W pudełku znajdują się tylko kule białe, kule czerwone i kule zielone. Prawdopodobieństwo wylosowania z pudełka kuli czerwonej jest dwa razy większe niż prawdopodobieństwo wylosowania kuli białej i dwa razy mniejsze niż wylosowanie kuli zielonej. Prawdopodobieństwo wylosowania z pudełka kuli białej jest równe
A) 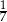 B)
B) 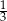 C)
C)  D)
D) 
Dana jest funkcja kwadratowa 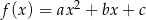 , gdzie
, gdzie 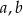 i
i  są liczbami rzeczywistymi takimi, że
są liczbami rzeczywistymi takimi, że 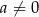 oraz
oraz 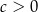 . Funkcja
. Funkcja 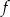 nie ma miejsc zerowych.
nie ma miejsc zerowych.
Dokończ zdanie tak, aby było prawdziwe. Wybierz odpowiedź A albo B oraz jej uzasadnienie 1, 2 albo 3.
Wykres funkcji 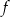 leży w całości
leży w całości
A) nad osią 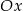 , , | B) pod osią 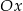 , , |
| ponieważ | |
| 1) | 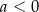 i i 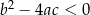 . . |
| 2) | 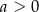 i i 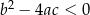 . . |
| 3) | 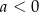 i i 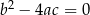 . . |
Na płaszczyźnie, w kartezjańskim układzie współrzędnych 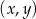 , dane są punkty
, dane są punkty 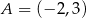 i
i 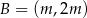 , gdzie
, gdzie 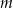 jest liczbą rzeczywistą, oraz prosta
jest liczbą rzeczywistą, oraz prosta 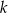 o równaniu
o równaniu 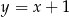 . Prosta przechodząca przez punkty
. Prosta przechodząca przez punkty 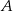 i
i 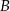 jest równoległa do prostej
jest równoległa do prostej 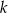 , gdy
, gdy
A) 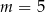 B)
B) 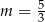 C)
C) 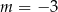 D)
D) 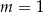
Podstawą graniastosłupa prostego jest romb o przekątnych długości 8 cm i 12 cm. Wysokość tego graniastosłupa jest dwa razy krótsza od dłuższej przekątnej rombu w podstawie. Wtedy objętość graniastosłupa jest równa
A) 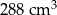 B)
B) 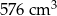 C)
C) 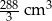 D)
D) 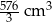
Jedna z przekątnych kwadratu 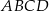 jest zawarta w prostej o równaniu
jest zawarta w prostej o równaniu 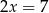 oraz
oraz 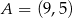 . Pole tego kwadratu jest równe
. Pole tego kwadratu jest równe
A) 121 B) 24,5 C) 60,5 D) 49
Informacja do zadań 30.1 i 30.2
Dach przybudówki przy hali magazynowej ma szerokość 25 metrów. Wysokość tego dachu w najniższym miejscu jest równa 5,4 m. Przekrój poprzeczny przybudówki przedstawiono poglądowo na rysunku. Wysokość dachu 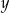 zmienia się wraz z odległością
zmienia się wraz z odległością  od hali magazynowej w sposób opisany funkcją:
od hali magazynowej w sposób opisany funkcją:
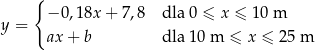
Wielkości  i
i  są wyrażone w metrach.
są wyrażone w metrach.
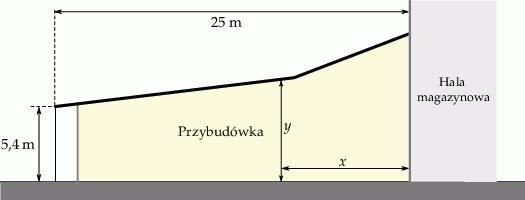
Wysokość dachu przybudówki w odległości 10 metrów od hali magazynowej jest równa
A) 7,2 m B) 6 m C) 8,4 m D) 9,6 m
Oblicz wartość współczynnika  oraz wartość współczynnika
oraz wartość współczynnika 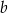 .
.
Rozważamy wszystkie równoległoboki o obwodzie równym 160 i kącie rozwartym o mierze 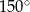 .
.
- Podaj wzór i dziedzinę funkcji opisującej zależność pola takiego równoległoboku od długości
 boku równoległoboku.
boku równoległoboku. - Oblicz wymiary tego z rozważanych równoległoboków, który ma największe pole, i oblicz to największe pole.
Informacja do zadań 32.1 i 32.2
Na diagramie przedstawiono oceny z pracy klasowej z matematyki w klasie IIa.
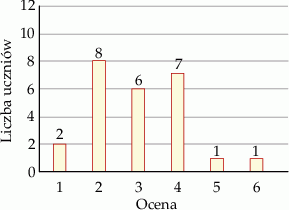
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Dominanta ocen otrzymanych z pracy klasowej jest mniejsza od 3. | P | F |
| Mediana ocen otrzymanych z pracy klasowej jest równa 3,5. | P | F |
Odchylenie standardowe danych przedstawionych na diagramie jest równe
A) 1,2 B) 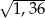 C)
C) 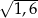 D) 1,6
D) 1,6

