Zadanie nr 7651016
Do obszaru kąta ostrego o mierze  należy punkt
należy punkt 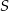 , którego odległości od ramion kąta są równe
, którego odległości od ramion kąta są równe  i
i 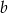 . Oblicz odległość punktu
. Oblicz odległość punktu 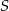 od wierzchołka kąta.
od wierzchołka kąta.
Rozwiązanie
Zaczynamy oczywiście od rysunku i przyjmijmy oznaczenia 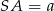 ,
, 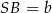 .
.
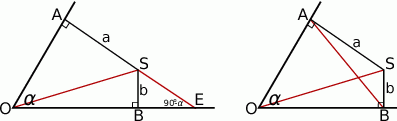
Sposób I
Zauważamy, że jeżeli przedłużymy odcinek 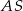 tak, aby przeciął drugie ramię kąta, powiedzmy w punkcie
tak, aby przeciął drugie ramię kąta, powiedzmy w punkcie 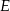 , to w otrzymanym trójkącie prostokątnym
, to w otrzymanym trójkącie prostokątnym 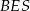 znamy kąt
znamy kąt 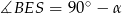 oraz przyprostokątną
oraz przyprostokątną 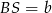 . Możemy więc obliczyć długość przeciwprostokątnej
. Możemy więc obliczyć długość przeciwprostokątnej
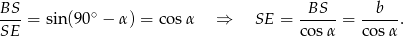
Teraz już łatwo, mamy 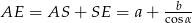 . Patrzymy teraz na trójkąt prostokątny
. Patrzymy teraz na trójkąt prostokątny 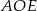 – znamy w nim jeden kąt i przyprostokątną. Możemy więc policzyć drugą przyprostokątną
– znamy w nim jeden kąt i przyprostokątną. Możemy więc policzyć drugą przyprostokątną
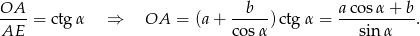
Pozostało policzyć długość odcinka 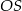 z trójkąta prostokątnego
z trójkąta prostokątnego 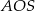 .
.
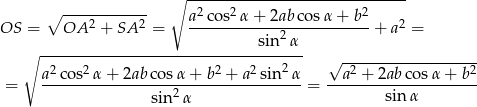
Sposób II
Tym razem przyjrzyjmy się czworokątowi 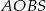 . Ponieważ ma on dwa przeciwległe kąty proste, można na nim opisać okrąg. Dokładniej, okrąg ten to okrąg o średnicy
. Ponieważ ma on dwa przeciwległe kąty proste, można na nim opisać okrąg. Dokładniej, okrąg ten to okrąg o średnicy 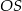 (bo
(bo 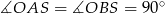 ). Musimy zatem obliczyć średnicę okręgu opisanego na czworokącie
). Musimy zatem obliczyć średnicę okręgu opisanego na czworokącie 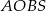 . Jak to zrobić? – najprościej z twierdzenia sinusów, do tego musimy jednak znać bok i przeciwległy kąt w którymkolwiek z trójkątów utworzonych przez wierzchołki tego czworokąta. Chwila zastanowienia i wiadomo co robić – w trójkącie
. Jak to zrobić? – najprościej z twierdzenia sinusów, do tego musimy jednak znać bok i przeciwległy kąt w którymkolwiek z trójkątów utworzonych przez wierzchołki tego czworokąta. Chwila zastanowienia i wiadomo co robić – w trójkącie 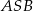 znamy kąt
znamy kąt 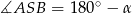 i łatwo możemy wyliczyć bok
i łatwo możemy wyliczyć bok 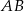 . Liczymy (z twierdzenia cosinusów).
. Liczymy (z twierdzenia cosinusów).
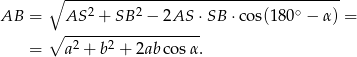
Pozostało skorzystać z twierdzenia sinusów
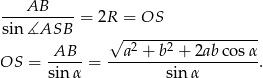
Odpowiedź: