/Szkoła średnia/Zadania maturalne/Matura 2023/Matura próbna
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis zadania.info poziom rozszerzony 1 kwietnia 2023 Czas pracy: 180 minut
Dane są liczby 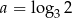 oraz
oraz 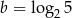 . Wyraź
. Wyraź 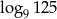 za pomocą
za pomocą  oraz
oraz 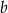 .
.
Informacja do zadań 2.1 i 2.2
Funkcja 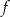 określona jest wzorem
określona jest wzorem
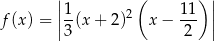
dla każdego 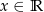 . Pochodna funkcji
. Pochodna funkcji 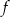 w punkcie
w punkcie 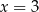 jest równa 0.
jest równa 0.
Wyznacz zbiór wszystkich wartości, jakie funkcja przyjmuje na przedziale ![[− 4 ,4 ]](https://img.zadania.info/zes/0045787/HzesT10x.gif) .
.
Wyznacz wszystkie wartości parametru 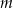 , dla których równanie
, dla których równanie 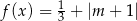 ma cztery rozwiązania, których iloczyn jest ujemny.
ma cztery rozwiązania, których iloczyn jest ujemny.
Dane są dwie urny z kulami. W każdej z urn jest siedem kul. W pierwszej urnie są trzy kule czarne i cztery kule białe, w drugiej urnie są dwie kule czarne i pięć białych. Rzucamy jeden raz symetryczną monetą. Jeżeli wypadnie reszka, to losujemy jedną kulę z pierwszej urny, w przeciwnym przypadku – jedną kulę z drugiej urny. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że w tym doświadczeniu wylosujemy kulę białą.
Udowodnij, że różnica sześcianów dwóch kolejnych liczb całkowitych nie jest liczbą podzielną przez 5.
Rozwiąż nierówność
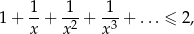
gdzie lewa strona jest sumą zbieżnego szeregu geometrycznego.
Wyznacz wszystkie wartości parametru 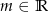 , dla których równanie
, dla których równanie
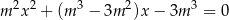
ma dwa różne rozwiązania rzeczywiste 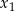 oraz
oraz 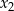 spełniające warunek
spełniające warunek
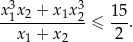
Rozwiąż równanie
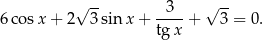
Dany jest trójkąt równoramienny 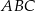 , w którym
, w którym 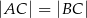 , a punkt
, a punkt 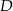 jest środkiem podstawy
jest środkiem podstawy 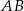 . Okrąg o środku
. Okrąg o środku 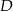 jest styczny do prostej
jest styczny do prostej 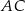 . Punkt
. Punkt 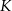 leży na boku
leży na boku 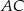 , punkt
, punkt 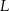 leży na boku
leży na boku 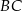 , odcinek
, odcinek 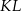 jest styczny do rozważanego okręgu oraz
jest styczny do rozważanego okręgu oraz 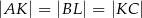 (zobacz rysunek).
(zobacz rysunek).
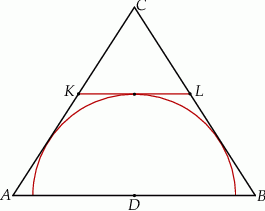
Wykaż, że trójkąt 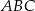 jest równoboczny.
jest równoboczny.
W kartezjańskim układzie współrzędnych 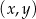 punkt
punkt 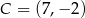 jest wierzchołkiem trójkąta
jest wierzchołkiem trójkąta 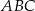 . Prosta
. Prosta 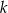 o równaniu
o równaniu 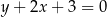 zawiera dwusieczną kąta
zawiera dwusieczną kąta 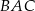 tego trójkąta. Okrąg
tego trójkąta. Okrąg 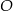 o równaniu
o równaniu 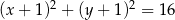 jest wpisany w ten trójkąt. Wyznacz współrzędne wierzchołków
jest wpisany w ten trójkąt. Wyznacz współrzędne wierzchołków 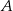 i
i 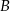 trójkąta
trójkąta 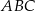 .
.
Dany jest graniastosłup prosty 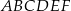 , którego podstawą jest trójkąt
, którego podstawą jest trójkąt 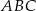 o kątach
o kątach 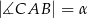 i
i 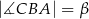 . Przekątne
. Przekątne 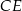 i
i 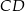 ścian bocznych tworzą kąt o mierze
ścian bocznych tworzą kąt o mierze 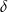 takiej, że
takiej, że 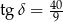 (zobacz rysunek).
(zobacz rysunek).
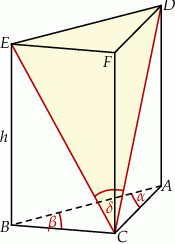
Pole trójkąta 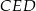 jest równe 4, a pole trójkąta
jest równe 4, a pole trójkąta 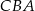 jest równe
jest równe 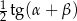 . Oblicz wysokość
. Oblicz wysokość 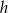 tego graniastosłupa.
tego graniastosłupa.
Budżet przeznaczony na ogrodzenie pewnej działki w kształcie trójkąta równoramiennego 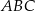 (
(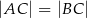 ) wynosi 12 000 zł.
) wynosi 12 000 zł.
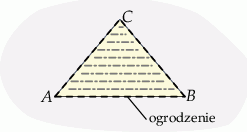
Ze względu na warunki terenowe, koszt wykonania 1 metra bieżącego ogrodzenia jest różny dla każdego z boków trójkąta 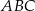 i wynosi odpowiednio: 140 zł dla boku
i wynosi odpowiednio: 140 zł dla boku 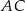 , 100 zł dla boku
, 100 zł dla boku 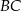 i 360 zł dla boku
i 360 zł dla boku 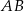 . Oblicz jakie powinny być wymiary ogrodzenia, aby odgradzało ono działkę o największym możliwym polu powierzchni. Wymiary podaj z dokładnością do 1 metra.
. Oblicz jakie powinny być wymiary ogrodzenia, aby odgradzało ono działkę o największym możliwym polu powierzchni. Wymiary podaj z dokładnością do 1 metra.

