/Szkoła średnia/Zadania maturalne/Matura 2023/Matura próbna
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis zadania.info poziom podstawowy 15 kwietnia 2023 Czas pracy: 180 minut
Wartość wyrażenia 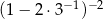 jest równa
jest równa
A) 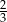 B)
B)  C) 9 D)
C) 9 D) 
Wartość liczbowa wyrażenia 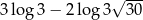 jest równa
jest równa
A) 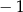 B) 2 C)
B) 2 C) 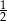 D)
D) 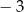
Punkty 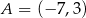 i
i 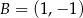 są sąsiednimi wierzchołkami kwadratu
są sąsiednimi wierzchołkami kwadratu 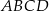 . Odcinek łączący środki dwóch sąsiednich boków tego kwadratu ma długość
. Odcinek łączący środki dwóch sąsiednich boków tego kwadratu ma długość
A) 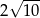 B)
B) 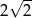 C)
C) 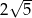 D)
D) 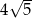
Na rysunku przedstawiony jest zbiór wszystkich liczb rzeczywistych spełniających nierówność 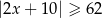 .
.
![]()
Stąd wynika, że
A) 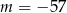 B)
B) 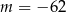 C)
C) 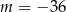 D)
D) 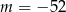
Po wykonaniu działań w wyrażeniu 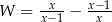 otrzymujemy
otrzymujemy
A) 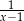 B)
B) 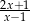 C)
C) 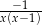 D)
D) 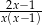
Równanie
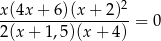
ma w zbiorze liczb rzeczywistych
A) dokładnie jedno rozwiązanie: 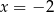 .
.
B) dokładnie dwa rozwiązania: 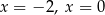 .
.
C) dokładnie trzy rozwiązania: 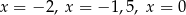 .
.
D) dokładnie cztery rozwiązania: 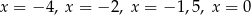 .
.
Na rysunku jest przedstawiony wykres funkcji 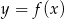 określonej na przedziale
określonej na przedziale ![[− 5,6]](https://img.zadania.info/zes/0089075/HzesT32x.gif) . Wykres ten przecina oś
. Wykres ten przecina oś 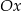 w punktach:
w punktach: 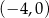 ,
, 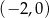 i
i 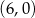 .
.
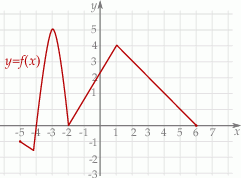
Wskaż zbiór rozwiązań nierówności 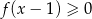 .
.
A) ![[− 3,7]](https://img.zadania.info/zes/0089075/HzesT39x.gif) B)
B) ![[− 4,− 2)∪ (− 2 ,6 ]](https://img.zadania.info/zes/0089075/HzesT40x.gif) C)
C) ![[−4 ,6]](https://img.zadania.info/zes/0089075/HzesT41x.gif) D)
D) ![[− 5,5]](https://img.zadania.info/zes/0089075/HzesT42x.gif)
Dane są takie liczby całkowite 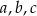 i
i 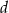 , dla których liczba
, dla których liczba 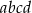 jest podzielna przez 3, ale nie jest podzielna przez 6. Wykaż, że liczba
jest podzielna przez 3, ale nie jest podzielna przez 6. Wykaż, że liczba
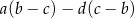
dzieli się przez 4.
Ciąg 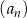 jest określony wzorem
jest określony wzorem 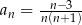 dla każdej liczby naturalnej
dla każdej liczby naturalnej 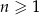 . Wynika stąd, że suma siedmiu początkowych wyrazów ciągu
. Wynika stąd, że suma siedmiu początkowych wyrazów ciągu 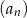 jest większa od sumy pięciu początkowych wyrazów ciągu
jest większa od sumy pięciu początkowych wyrazów ciągu 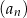 o
o
A) 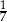 B)
B) 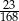 C)
C) 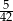 D) 0
D) 0
Zbiór rozwiązań nierówności kwadratowej 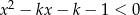 z niewiadomą
z niewiadomą  i parametrem
i parametrem 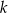 , jest taki sam jak zbiór rozwiązań nierówności
, jest taki sam jak zbiór rozwiązań nierówności 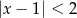 . Liczba
. Liczba 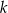 jest równa
jest równa
A) 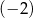 B) 2 C)
B) 2 C) 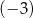 D) 3
D) 3
Dane są dwa trójkąty podobne 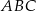 i
i 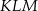 o polach równych – odpowiednio –
o polach równych – odpowiednio – 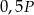 oraz
oraz 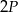 . Promień okręgu wpisanego w trójkąt
. Promień okręgu wpisanego w trójkąt 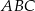 jest równy
jest równy  .
.
Dokończ zdanie tak, aby było prawdziwe. Wybierz odpowiedź A albo B oraz jej uzasadnienie 1, 2 albo 3.
Promień okręgu wpisanego w trójkąt 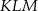 jest równy
jest równy
A) 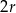 , , | B) 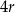 , , |
| ponieważ stosunek promieni okręgów wpisanych trójkątów podobnych jest równy | |
| 1) | pierwiastkowi kwadratowemu ze stosunku pól tych trójkątów. |
| 2) | kwadratowi stosunku pól tych trójkątów. |
| 3) | stosunkowi pól tych trójkątów. |
Dany jest wielomian 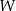 określony wzorem
określony wzorem 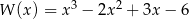 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Wielomian
. Wielomian 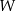 przy rozkładzie na czynniki ma postać
przy rozkładzie na czynniki ma postać
A) 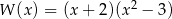 B)
B) 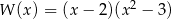
C) 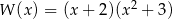 D)
D) 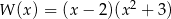
Jeżeli 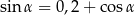 to liczba
to liczba 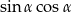 jest równa
jest równa
A) 0,6 B) 0,3 C) 0,96 D) 0,48
W pewnym obszarze leśnym początkowo rosło 10 000 trzydziestoletnich buków. Na tym obszarze rozpoczęto wyrąb tych drzew i przez 3 kolejne lata wycinano 10% pozostałych buków. Po 3 latach od rozpoczęcia wycinki liczba pozostałych buków jest równa
A) 7000 B) 8100 C) 6561 D) 7290
Na płaszczyźnie, w kartezjańskim układzie współrzędnych 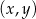 , dane są:
, dane są:
– prosta 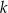 o równaniu
o równaniu 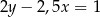
– prosta 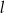 o równaniu
o równaniu 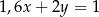 . Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Proste 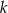 i i 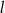 przecinają się pod kątem przecinają się pod kątem 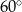 . . | P | F |
Punkt wspólny prostych 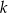 i i 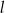 ma obie współrzędne całkowite. ma obie współrzędne całkowite. | P | F |
Uzasadni, że jeżeli liczby rzeczywiste 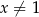 ,
, 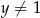 i
i 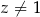 spełniają warunki:
spełniają warunki: 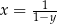 i
i 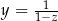 , to
, to 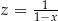 .
.
Proste o równaniach 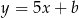 i
i 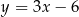 przecinają się w punkcie leżącym na osi
przecinają się w punkcie leżącym na osi 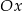 . Zatem
. Zatem
A) 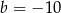 B)
B) 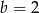 C)
C) 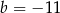 D)
D) 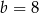
Dokończ zdanie. Wybierz dwie właściwe odpowiedzi spośród podanych.
Dla wszystkich liczb rzeczywistych 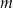 ,
,  i
i 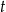 wyrażenie
wyrażenie 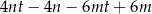 jest równe
jest równe
A) 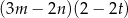 B)
B) 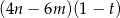
C) 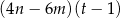 D)
D) 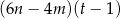
E) 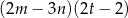 F)
F) 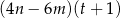
Informacja do zadań 19.1 i 19.2
Dany jest ciąg 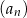 określony wzorem
określony wzorem 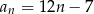 dla każdej liczby naturalnej
dla każdej liczby naturalnej 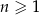 .
.
Najmniejszą wartością  , dla której wyraz
, dla której wyraz 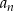 jest większy od 2023, jest
jest większy od 2023, jest
A) 170 B) 169 C) 168 D) 203
Suma  początkowych wyrazów ciągu
początkowych wyrazów ciągu 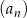 jest równa 145 dla
jest równa 145 dla  równego
równego
A) 6 B) 23 C) 5 D) 11
Do wyznaczenia boków pewnego kąpieliska w kształcie prostokąta należy użyć liny o długości 80 m. Część jednego z boków tego kąpieliska będzie pokrywać się z końcem pomostu i na tym odcinku lina nie jest potrzebna (zobacz rysunek). Pomost ma szerokość 4 metrów.
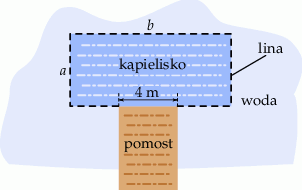
Oblicz wymiary  i
i 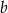 kąpieliska tak, aby jego powierzchnia była największa.
kąpieliska tak, aby jego powierzchnia była największa.
Informacja do zadań 21.1 i 21.2
Funkcja kwadratowa 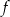 jest określona wzorem
jest określona wzorem 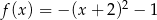 .
.
Wykresem funkcji 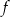 jest parabola, której wierzchołek ma współrzędne
jest parabola, której wierzchołek ma współrzędne
A) 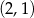 B)
B) 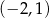 C)
C) 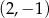 D)
D) 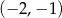
Zbiorem wartości funkcji 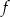 jest przedział
jest przedział
A) ![(− ∞ ,− 1]](https://img.zadania.info/zes/0089075/HzesT133x.gif) B)
B) ![(− ∞ ,1]](https://img.zadania.info/zes/0089075/HzesT134x.gif) C)
C) 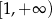 D)
D) 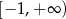
W pojemniku znajdują się losy loterii fantowej ponumerowane kolejnymi liczbami naturalnymi od 2000 do 7000. Każdy los, którego numer jest liczbą o sumie cyfr równej 4, jest wygrywający. Uczestnicy loterii losują z pojemnika po jednym losie. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że pierwszy los wyciągnięty z pojemnika był wygrywający.
Odcinki 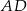 i
i 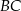 przecinają się w punkcie
przecinają się w punkcie 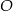 . W trójkątach
. W trójkątach 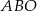 i
i 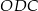 zachodzą związki:
zachodzą związki: 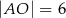 ,
, 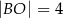 ,
, 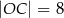 ,
, 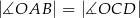 (zobacz rysunek).
(zobacz rysunek).
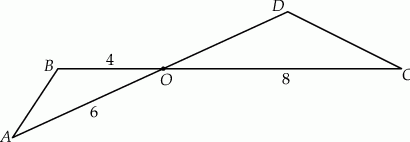
Oblicz długość boku 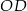 trójkąta
trójkąta 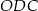 .
.
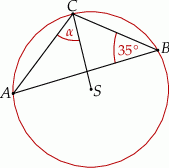
Punkt 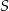 jest środkiem okręgu (patrz rysunek). Zaznaczony kąt
jest środkiem okręgu (patrz rysunek). Zaznaczony kąt  jest równy
jest równy
A) 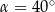 B)
B) 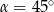 C)
C) 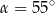 D)
D) 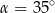
Informacja do zadań 25.1 i 25.2
Na rysunku przedstawiony jest czworościan foremny 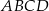 , którego objętość i pole powierzchni całkowitej są odpowiednio równe:
, którego objętość i pole powierzchni całkowitej są odpowiednio równe: 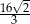 i
i 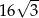 .
.
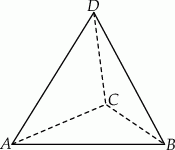
Promień okręgu wpisanego w ścianę 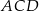 jest równy
jest równy
A) 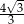 B)
B) 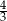 C)
C) 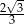 D)
D) 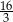
Wysokość czworościanu 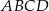 jest równa
jest równa
A) 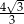 B)
B) 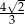 C)
C) 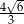 D)
D) 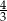
Ciąg 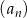 , określony dla każdej liczby naturalnej
, określony dla każdej liczby naturalnej 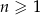 , jest arytmetyczny. Różnica tego ciągu jest równa 3 oraz
, jest arytmetyczny. Różnica tego ciągu jest równa 3 oraz 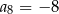 . Czwarty wyraz tego ciągu jest równy
. Czwarty wyraz tego ciągu jest równy
A) 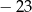 B)
B) 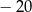 C)
C) 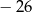 D)
D) 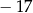
Na płaszczyźnie, w kartezjańskim układzie współrzędnych 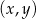 , dany jest okrąg
, dany jest okrąg 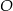 o równaniu
o równaniu
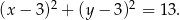
Okrąg 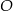 przecina oś
przecina oś 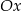 w punktach o współrzędnych
w punktach o współrzędnych
A) 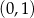 i
i 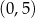 B)
B) 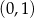 i
i 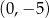
C) 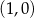 i
i 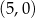 D)
D) 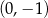 i
i 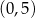
Liczba  jest dodatnia. Mediana zestawu czterech liczb:
jest dodatnia. Mediana zestawu czterech liczb: 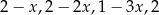 , jest równa
, jest równa 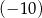 . Wtedy
. Wtedy
A) 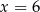 B)
B) 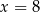 C)
C) 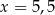 D)
D) 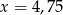
Ze zbioru liczb naturalnych pięciocyfrowych losujemy jedną liczbę. Prawdopodobieństwo zdarzenia polegającego na tym, że wylosowana liczba jest podzielna przez 5, jest równe
A)  B)
B) 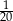 C)
C) 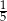 D)
D) 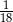
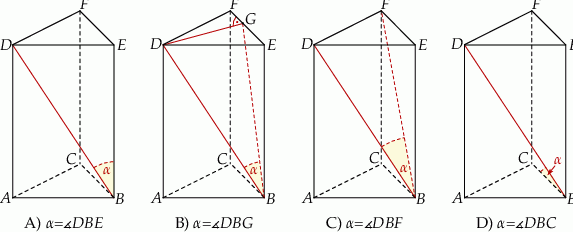
Dany jest graniastosłup prawidłowy trójkątny 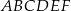 . Na którym z rysunków prawidłowo narysowano, oznaczono i podpisano kąt
. Na którym z rysunków prawidłowo narysowano, oznaczono i podpisano kąt  pomiędzy ścianą boczną
pomiędzy ścianą boczną 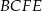 i przekątną
i przekątną 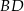 ściany bocznej
ściany bocznej 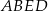 tego graniastosłupa?
tego graniastosłupa?
Wierzchołki rombu  leżą na bokach trójkąta
leżą na bokach trójkąta  , przy czym boki
, przy czym boki  i
i 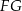 są równoległe do środkowej
są równoległe do środkowej 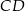 trójkąta
trójkąta 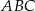 (zobacz rysunek).
(zobacz rysunek).
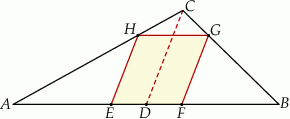
Oblicz długość boku rombu 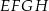 jeżeli
jeżeli 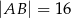 i
i 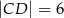 .
.
Informacja do zadań 32.1 i 32.2
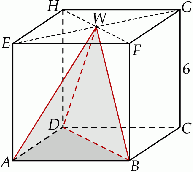
Dany jest sześcian 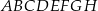 o krawędzi długości 6. Wierzchołki
o krawędzi długości 6. Wierzchołki 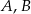 i
i 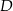 podstawy
podstawy 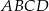 sześcianu połączono odcinkami z punktem
sześcianu połączono odcinkami z punktem 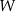 , który jest punktem przecięcia przekątnych podstawy
, który jest punktem przecięcia przekątnych podstawy 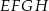 . Otrzymano w ten sposób ostrosłup trójkątny
. Otrzymano w ten sposób ostrosłup trójkątny 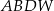 .
.
Objętość 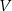 ostrosłupa
ostrosłupa 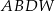 jest równa
jest równa
A) 108 B) 72 C) 216 D) 36
Oblicz cosinus kąta ostrego jaki tworzą krawędzie 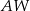 i
i 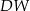 ostrosłupa.
ostrosłupa.

