/Szkoła średnia/Zadania maturalne/Matura 2023/Matura próbna
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis zadania.info poziom podstawowy 29 kwietnia 2023 Czas pracy: 180 minut
Liczba 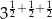 jest równa
jest równa
A) 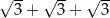 B)
B) 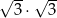 C)
C) 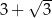 D)
D) 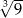
Wartość wyrażenia 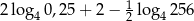 jest równa
jest równa
A) 0 B) 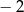 C) 2 D) 4
C) 2 D) 4
Kwotę 10 000 zł ulokowano w banku na dwuletnią lokatę oprocentowaną w wysokości 5% w stosunku rocznym. Co pół roku środki zgromadzone na lokacie są powiększane o odsetki, od których odprowadzany jest podatek w wysokości 19%. Maksymalna kwota, jaką po upływie dwóch lat będzie można wypłacić z banku, jest równa
A) 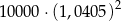 B)
B) 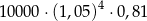
C) 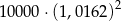 D)
D) 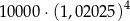
Dla każdej liczby rzeczywistej 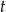 wartość wyrażenia
wartość wyrażenia 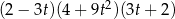 jest równa
jest równa
A) 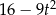 B)
B) 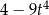 C)
C) 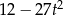 D)
D) 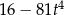
Informacja do zadań 5.1 i 5.2
Na rysunku, w kartezjańskim układzie współrzędnych  , przedstawiono wykres funkcji
, przedstawiono wykres funkcji  określonej dla każdego
określonej dla każdego ![x ∈ (− 6,5]](https://img.zadania.info/zes/0094150/HzesT19x.gif) . Na tym wykresie zaznaczono punkty o współrzędnych całkowitych.
. Na tym wykresie zaznaczono punkty o współrzędnych całkowitych.
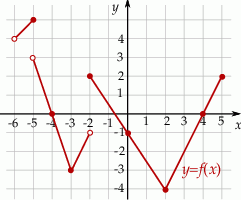
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Funkcja 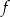 jest malejąca na przedziale jest malejąca na przedziale ![[− 2,2]](https://img.zadania.info/zes/0094150/HzesT22x.gif) . . | P | F |
Dla każdego argumentu z przedziału ![[− 4,− 2]](https://img.zadania.info/zes/0094150/HzesT23x.gif) funkcja funkcja 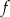 przyjmuje wartości niedodatnie. przyjmuje wartości niedodatnie. | P | F |
Wyznacz zbiór wartości funkcji 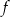 .
.
Wszystkich różnych liczb naturalnych czterocyfrowych, w których zapisie dziesiętnym występują cztery różne cyfry parzyste jest
A) 120 B) 96 C) 625 D) 500
Wykaż, że jeżeli liczba  nie dzieli się przez 3, to liczba
nie dzieli się przez 3, to liczba 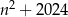 jest podzielna przez 3.
jest podzielna przez 3.
Informacja do zadań 8.1 i 8.2
W kartezjańskim układzie współrzędnych dane są punkty: 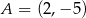 ,
, 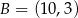 i
i 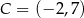 .
.
Dokończ zdanie tak, aby było prawdziwe. Wybierz odpowiedź A, B albo C oraz jej uzasadnienie 1, 2 albo 3.
Punkty 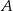 ,
, 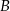 i
i 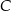
| A) | są współliniowe, |
| B) | są wierzchołkami trójkąta prostokątnego, |
| C) | są wierzchołkami trójkąta równoramiennego, |
ponieważ
1) 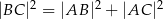 , , | 2) 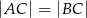 , , | 3) 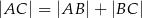 , , |
Środek odcinka łączącego punkt 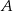 ze środkiem odcinka
ze środkiem odcinka 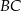 ma współrzędne
ma współrzędne
A) 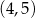 B)
B) 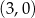 C)
C) 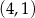 D)
D) 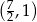
Dana jest funkcja liniowa 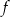 określona wzorem
określona wzorem 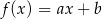 , gdzie
, gdzie  i
i 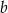 są liczbami rzeczywistymi. Wykres funkcji
są liczbami rzeczywistymi. Wykres funkcji 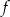 przedstawiono w kartezjańskim układzie współrzędnych
przedstawiono w kartezjańskim układzie współrzędnych 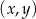 na rysunku poniżej
na rysunku poniżej
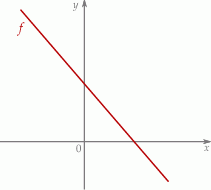
Współczynniki  i
i 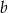 we wzorze funkcji
we wzorze funkcji 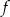 spełniają warunki
spełniają warunki
A) 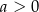 i
i 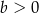 B)
B) 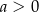 i
i 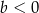 C)
C) 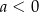 i
i 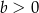 D)
D) 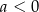 i
i 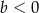
Dla każdej dodatniej liczby 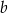 wyrażenie
wyrażenie 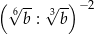 jest równe
jest równe
A) 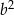 B)
B) 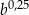 C)
C) 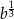 D)
D) 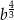
Wartość wyrażenia 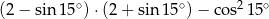 jest równa
jest równa
A) 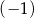 B) 3 C) 15 D) 0
B) 3 C) 15 D) 0
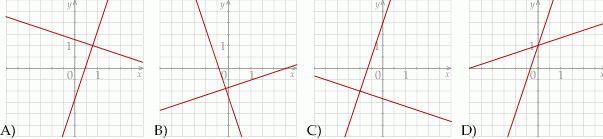
Dany jest układ równań
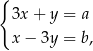
gdzie  i
i 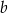 są pewnymi liczbami rzeczywistymi. Na którym z rysunków może być przedstawiona interpretacja geometryczna tego układu równań?
są pewnymi liczbami rzeczywistymi. Na którym z rysunków może być przedstawiona interpretacja geometryczna tego układu równań?
Rozwiąż równanie 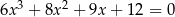 .
.
Dwa krótsze boki trójkąta rozwartokątnego 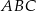 mają długości
mają długości 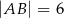 i
i 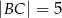 . Sinus największego kąta tego trójkąta jest równy
. Sinus największego kąta tego trójkąta jest równy 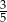 . Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Pole trójkąta 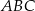 jest mniejsze od 10. jest mniejsze od 10. | P | F |
Cosinus kąta 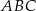 trójkąta trójkąta 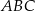 jest równy jest równy  . . | P | F |
Iloczyn wszystkich rozwiązań równania 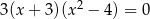 jest równy
jest równy
A) 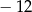 B)
B) 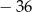 C) 36 D) 12
C) 36 D) 12
Dany jest ciąg arytmetyczny 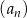 , określony dla każdej liczby naturalnej
, określony dla każdej liczby naturalnej 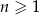 . W tym ciągu
. W tym ciągu 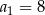 ,
, 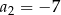 ,
, 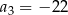 .
.
Dokończ zdanie. Wybierz dwie właściwe odpowiedzi spośród podanych.
Wzór ogólny ciągu 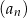 ma postać
ma postać
A) 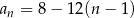 B)
B) 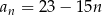
C) 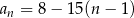 D)
D) 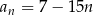
E) 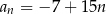 F)
F) 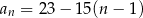
Dany jest ciąg 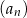 określony wzorem
określony wzorem 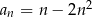 dla każdej liczby naturalnej
dla każdej liczby naturalnej 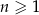 . Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Ciąg 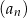 jest malejący. jest malejący. | P | F |
Siódmy wyraz ciągu 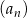 jest równy jest równy 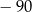 . . | P | F |
Przez punkt przecięcia wysokości trójkąta równobocznego 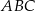 poprowadzono prostą
poprowadzono prostą 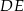 równoległą do podstawy
równoległą do podstawy 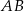 (zobacz rysunek).
(zobacz rysunek).
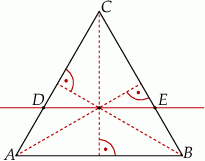
Stosunek pola trójkąta 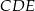 do pola trapezu
do pola trapezu 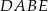 jest równy
jest równy
A) 5 : 9 B) 4 : 5 C) 4 : 9 D) 3 : 2
Tekturowy karton ma mieć kształt prostopadłościanu, którego podstawa jest prostokątem o jednym z boków dłuższym od drugiego o 24 cm. Suma wszystkich krawędzi tego prostopadłościanu ma być równa 480 cm.
- Napisz wzór funkcji
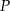 wyrażającej całkowite pole zewnętrznej powierzchni kartonu, w zależności od długości
wyrażającej całkowite pole zewnętrznej powierzchni kartonu, w zależności od długości  krótszej krawędzi jego podstawy. Podaj dziedzinę funkcji
krótszej krawędzi jego podstawy. Podaj dziedzinę funkcji 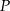 .
. - Oblicz jakie powinny być wymiary tego kartonu tak, aby łączne pole powierzchni jego ścian było największe możliwe.
Informacja do zadań 20.1 – 20.3
Dana jest funkcja kwadratowa 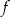 , której fragment wykresu przedstawiono na rysunku poniżej. Wykresem funkcji
, której fragment wykresu przedstawiono na rysunku poniżej. Wykresem funkcji 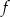 jest parabola, której punkty przecięcia z osiami układu współrzędnych mają współrzędne całkowite.
jest parabola, której punkty przecięcia z osiami układu współrzędnych mają współrzędne całkowite.
Funkcja  jest określona za pomocą funkcji
jest określona za pomocą funkcji  następująco:
następująco: 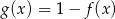 . Wykres funkcji
. Wykres funkcji 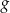 przedstawiono na rysunku
przedstawiono na rysunku
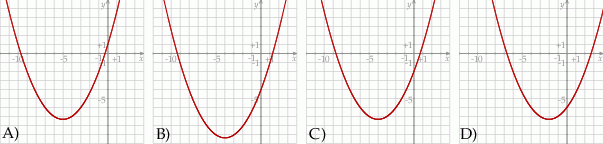
Rozwiąż nierówność 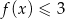 .
.
Wyznacz zbiór wartości funkcji 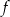 .
.
Odcinek 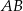 jest średnicą okręgu o środku w punkcie
jest średnicą okręgu o środku w punkcie 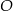 i promieniu
i promieniu 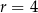 (zobacz rysunek). Cięciwa
(zobacz rysunek). Cięciwa 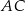 ma długość
ma długość 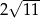 .
.
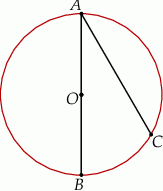
Sinus kąta 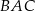 jest równy
jest równy
A) 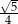 B)
B) 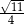 C)
C) 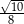 D)
D) 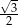
Ze zbioru ośmioelementowego 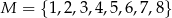 losujemy kolejno ze zwracaniem dwa razy po jednej liczbie. Zdarzenie
losujemy kolejno ze zwracaniem dwa razy po jednej liczbie. Zdarzenie 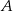 polega na wylosowaniu dwóch liczb ze zbioru
polega na wylosowaniu dwóch liczb ze zbioru 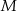 , których iloczyn jest równy 24. Oblicz prawdopodobieństwo zdarzenia
, których iloczyn jest równy 24. Oblicz prawdopodobieństwo zdarzenia 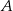 .
.
Na płaszczyźnie, w kartezjańskim układzie współrzędnych 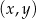 , dane są proste
, dane są proste 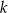 oraz
oraz 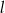 o równaniach
o równaniach
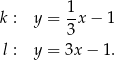
Proste 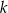 oraz
oraz 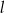
A) nie mają punktów wspólnych. B) są prostopadłe.
C) przecinają się w punkcie 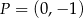 . D) pokrywają się.
. D) pokrywają się.
Dany jest ciąg geometryczny 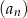 , określony dla każdej liczby naturalnej
, określony dla każdej liczby naturalnej 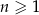 . Drugi wyraz tego ciągu oraz iloraz ciągu
. Drugi wyraz tego ciągu oraz iloraz ciągu 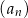 są równe
są równe 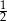 . Suma pięciu początkowych kolejnych wyrazów tego ciągu jest równa
. Suma pięciu początkowych kolejnych wyrazów tego ciągu jest równa
A) 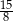 B)
B) 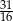 C)
C) 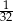 D)
D) 
Jedną z liczb spełniających nierówność 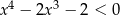 jest
jest
A) 3 B) 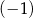 C) 2 D)
C) 2 D) 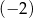
Cięciwy 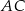 i
i 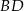 okręgu o środku
okręgu o środku 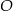 przecinają się w punkcie
przecinają się w punkcie 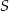 . Ponadto
. Ponadto 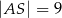 ,
, 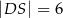 i
i 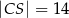 (zobacz rysunek).
(zobacz rysunek).
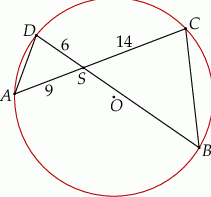
Długość odcinka 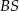 jest równa
jest równa
A) 24 B) 20 C) 21 D) 18
Jeżeli 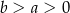 to wyrażenie
to wyrażenie 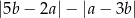 jest równe
jest równe
A) 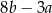 B)
B) 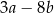 C)
C) 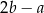 D)
D) 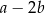
Dany jest trójkąt prostokątny o kącie prostym przy wierzchołku 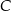 . Środkowa
. Środkowa 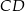 tworzy z przyprostokątną
tworzy z przyprostokątną 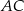 kąt
kąt 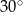 . Wynika stąd, że kąt między tą środkową a wysokością
. Wynika stąd, że kąt między tą środkową a wysokością 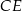 trójkąta ma miarę
trójkąta ma miarę
A) 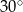 B)
B) 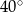 C)
C) 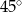 D)
D) 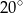
Dany jest trójkąt 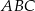 o bokach długości 6, 7 oraz 8. Oblicz cosinus najmniejszego kąta tego trójkąta.
o bokach długości 6, 7 oraz 8. Oblicz cosinus najmniejszego kąta tego trójkąta.
Powierzchnię boczną graniastosłupa prawidłowego czworokątnego o objętości 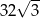 rozcięto wzdłuż krawędzi bocznej graniastosłupa i rozłożono na płaszczyźnie. Otrzymano w ten sposób prostokąt
rozcięto wzdłuż krawędzi bocznej graniastosłupa i rozłożono na płaszczyźnie. Otrzymano w ten sposób prostokąt 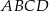 , w którym bok
, w którym bok 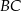 odpowiada krawędzi rozcięcia (wysokości graniastosłupa), a przekątna
odpowiada krawędzi rozcięcia (wysokości graniastosłupa), a przekątna 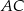 tworzy z bokiem
tworzy z bokiem 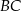 kąt o mierze
kąt o mierze 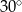 (zobacz rysunek).
(zobacz rysunek).
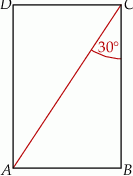
Długość krawędzi podstawy tego graniastosłupa jest równa.
A) 4 B) 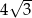 C)
C) 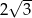 D) 2
D) 2
Informacja do zadań 31.1 i 31.2
W układzie współrzędnych dany jest okrąg  opisany równaniem
opisany równaniem 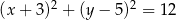 .
.
Pole trójkąta równobocznego wpisanego w ten okrąg jest równe
A) 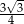 B) 6 C)
B) 6 C) 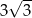 D)
D) 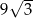
Sprawdź, czy prosta o równaniu 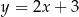 jest styczna do okręgu
jest styczna do okręgu  .
.

