/Szkoła średnia/Zadania maturalne/Matura 2023/Polygon matematyczny
Planimetria – czworokąty poziom rozszerzony
Prosta przechodząca przez wierzchołek 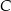 kwadratu
kwadratu 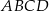 przecina przedłużenia jego boków
przecina przedłużenia jego boków 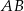 i
i 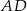 odpowiednio w punktach
odpowiednio w punktach 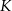 i
i 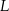 (zobacz rysunek).
(zobacz rysunek).
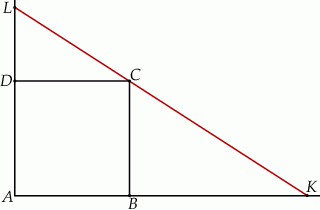
Wykaż, że
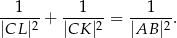
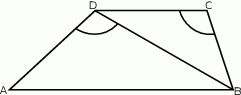
W trapezie 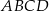 długość podstawy
długość podstawy 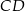 jest równa 18, a długości ramion trapezu
jest równa 18, a długości ramion trapezu 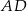 i
i 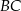 są odpowiednio równe 25 i 15. Kąty
są odpowiednio równe 25 i 15. Kąty 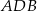 i
i 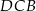 , zaznaczone na rysunku, mają równe miary. Oblicz obwód tego trapezu.
, zaznaczone na rysunku, mają równe miary. Oblicz obwód tego trapezu.
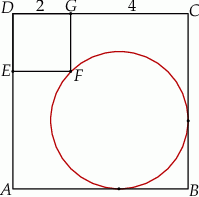
Na rysunku przedstawiono dwa kwadraty: 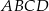 i
i 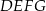 , przy czym punkty
, przy czym punkty 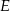 i
i 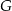 należą do odcinków
należą do odcinków 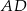 i
i 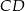 odpowiednio. Przedstawiono również okrąg, który jest styczny do dwóch boków kwadratu
odpowiednio. Przedstawiono również okrąg, który jest styczny do dwóch boków kwadratu 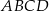 i przechodzi przez punkt
i przechodzi przez punkt 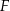 . Wykaż, że jeżeli
. Wykaż, że jeżeli 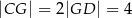 , to promień okręgu jest równy
, to promień okręgu jest równy 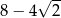 .
.
Kąt ostry rombu 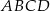 ma miarę
ma miarę 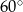 . Na bokach
. Na bokach 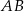 i
i 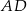 tego rombu wybrano punkty – odpowiednio –
tego rombu wybrano punkty – odpowiednio – 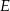 i
i 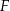 takie, że
takie, że 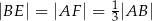 . Odcinki
. Odcinki 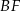 i
i 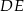 przecinają się w punkcie
przecinają się w punkcie 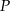 (zobacz rysunek).
(zobacz rysunek).
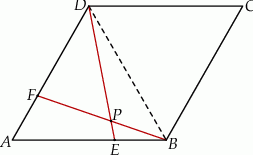
Wykaż, że punkt 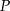 leży na okręgu opisanym na trójkącie
leży na okręgu opisanym na trójkącie 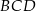 .
.
W trapezie 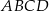 połączono środek
połączono środek 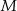 ramienia trapezu
ramienia trapezu 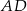 z końcami drugiego ramienia
z końcami drugiego ramienia 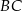 . Wykaż, że pole powstałego trójkąta
. Wykaż, że pole powstałego trójkąta 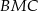 jest równe połowie pola trapezu
jest równe połowie pola trapezu 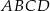 .
.
W czworokącie wypukłym 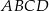 kąty przy wierzchołkach
kąty przy wierzchołkach 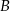 i
i 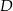 są proste (zobacz rysunek).
są proste (zobacz rysunek).
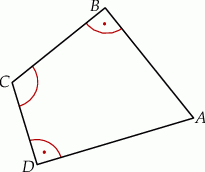
Oblicz sinus kąta przy wierzchołku 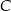 jeżeli
jeżeli 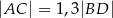 .
.
Sinus kąta jaki tworzą przekątne prostokąta o polu 60 jest równy 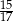 . Oblicz obwód tego prostokąta.
. Oblicz obwód tego prostokąta.
Kąt ostry równoległoboku ma miarę 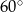 . Stosunek kwadratów długości przekątnych jest równy
. Stosunek kwadratów długości przekątnych jest równy 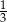 . Wykaż, że ten równoległobok jest rombem.
. Wykaż, że ten równoległobok jest rombem.
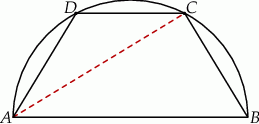
W półkole o promieniu  wpisano trapez równoramienny o krótszej podstawie długości
wpisano trapez równoramienny o krótszej podstawie długości  . Oblicz długość przekątnej trapezu.
. Oblicz długość przekątnej trapezu.
Różnica kwadratów długości przekątnych trapezu prostokątnego wynosi 21, jego wysokość ma długość 4, a dłuższe ramię ma długość 5. Oblicz pole trapezu.
Dany jest czworokąt wypukły 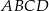 niebędący równoległobokiem. Punkty
niebędący równoległobokiem. Punkty 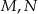 są odpowiednio środkami boków
są odpowiednio środkami boków 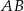 i
i 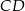 . Punkty
. Punkty 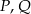 są odpowiednio środkami przekątnych
są odpowiednio środkami przekątnych 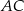 i
i 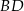 . Uzasadnij, że czworokąt
. Uzasadnij, że czworokąt 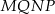 jest równoległobokiem.
jest równoległobokiem.
Trapez równoramienny 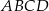 jest opisany na okręgu o promieniu
jest opisany na okręgu o promieniu  . Przekątna trapezu tworzy z dłuższą podstawą kąt
. Przekątna trapezu tworzy z dłuższą podstawą kąt  . Wyznacz obwód tego trapezu.
. Wyznacz obwód tego trapezu.
W dany trapez można wpisać okrąg i jednocześnie można na tym trapezie opisać okrąg. Wysokość tego trapezu jest równa 8, a jego kąt ostry ma miarę 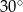 . Oblicz długość promienia okręgu opisanego na tym trapezie.
. Oblicz długość promienia okręgu opisanego na tym trapezie.
Czworokąt 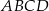 jest wpisany w okrąg o promieniu
jest wpisany w okrąg o promieniu 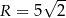 . Przekątna
. Przekątna 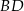 tego czworokąta ma długość 10. Kąty wewnętrzne
tego czworokąta ma długość 10. Kąty wewnętrzne 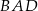 i
i 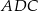 czworokąta
czworokąta 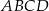 są ostre, a iloczyn sinusów wszystkich jego kątów wewnętrznych jest równy
są ostre, a iloczyn sinusów wszystkich jego kątów wewnętrznych jest równy 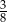 . Oblicz miary kątów wewnętrznych tego czworokąta.
. Oblicz miary kątów wewnętrznych tego czworokąta.

