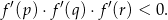/Szkoła średnia/Zadania maturalne/Matura 2023/Polygon matematyczny
Dowodzenie nierówności
Wykaż, że dla każdej liczby rzeczywistej  i każdej liczby rzeczywistej
i każdej liczby rzeczywistej 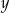 takich, że
takich, że 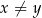 prawdziwa jest nierówność
prawdziwa jest nierówność
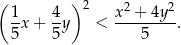
Wykaż, że dla dowolnej liczby 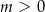 prawdziwa jest nierówność
prawdziwa jest nierówność 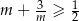 .
.
Wykaż, ze dla dowolnych liczb rzeczywistych 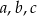 prawdziwa jest nierówność
prawdziwa jest nierówność
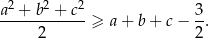
Udowodnij, że dla każdej liczby rzeczywistej  i każdej liczby rzeczywistej
i każdej liczby rzeczywistej 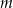 prawdziwa jest nierówność
prawdziwa jest nierówność 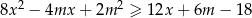 .
.
Wykaż, że dla dowolnych liczb rzeczywistych 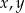 prawdziwa jest nierówność
prawdziwa jest nierówność
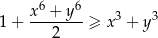
Wykaż, że dla dowolnych liczb rzeczywistych 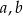 prawdziwa jest nierówność
prawdziwa jest nierówność
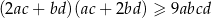
Udowodnij, że jeżeli 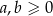 , to prawdziwa jest nierówność
, to prawdziwa jest nierówność 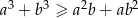 .
.
Wykaż, że dla dowolnych dodatnich liczb rzeczywistych  i
i 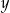 takich, że
takich, że 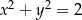 , prawdziwa jest nierówność
, prawdziwa jest nierówność 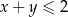 .
.
Wykaż, że dla każdej liczby rzeczywistej  i dla każdej liczby rzeczywistej
i dla każdej liczby rzeczywistej 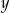 takich, że
takich, że 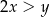 , spełniona jest nierówność
, spełniona jest nierówność
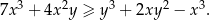
Wykaż, że dla wszystkich liczb rzeczywistych 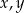 prawdziwa jest nierówność
prawdziwa jest nierówność 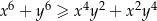 .
.
Uzasadnij, że jeśli liczby rzeczywiste 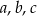 spełniają nierówności:
spełniają nierówności: 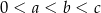 , to
, to
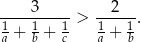
Niech 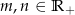 , udowodnij, że jeżeli
, udowodnij, że jeżeli 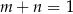 to prawdziwa jest nierówność
to prawdziwa jest nierówność 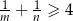 .
.
Udowodnij, że dla dowolnych różnych liczb rzeczywistych 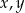 prawdziwa jest nierówność
prawdziwa jest nierówność
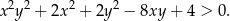
Udowodnij, że dla każdych dwóch liczb rzeczywistych 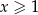 i
i 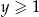 prawdziwa jest nierówność
prawdziwa jest nierówność
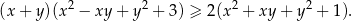
Wykaż, że jeżeli 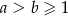 , to
, to 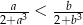 .
.
Wykaż, że dla dowolnej liczby rzeczywistej  spełniona jest nierówność
spełniona jest nierówność
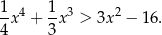
Wykaż, że dla każdej liczby rzeczywistej  prawdziwa jest nierówność:
prawdziwa jest nierówność:
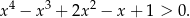
Funkcja 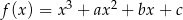 ma trzy różne miejsca zerowe:
ma trzy różne miejsca zerowe: 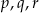 . Wykaż, że
. Wykaż, że