/Szkoła średnia/Zadania maturalne/Matura 2023/Polygon matematyczny

Stereometria – pole, kąty, odcinki poziom rozszerzony

Zadanie 1

Pole powierzchni bocznej ostrosłupa prawidłowego trójkątnego jest równe 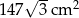√ -- 14 7 3 cm 2 , a pole jego powierzchni całkowitej wynosi 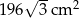√ -- 196 3 cm 2 . Oblicz długość krawędzi podstawy i długość krawędzi bocznej tego ostrosłupa.

Zadanie 2

Ściany boczne ostrosłupa prawidłowego trójkątnego są trójkątami o przyprostokątnych długości 12 cm. Oblicz objętość i pole powierzchni całkowitej tego ostrosłupa.

Zadanie 3

Pole podstawy graniastosłupa prawidłowego czworokątnego jest równe 16. Przekątna graniastosłupa jest nachylona do płaszczyzny jego podstawy pod kątem, którego sinus jest równy 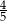4 5 . Oblicz pole powierzchni całkowitej tego graniastosłupa.

Zadanie 4

Oblicz cosinus kąta jaki tworzą dwie ściany czworościanu foremnego. Podaj przybliżoną miarę tego kąta.

Zadanie 5

Dany jest ostrosłup prawidłowy czworokątny o wysokości 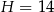H = 1 4 . Cosinus kąta nachylenia krawędzi bocznej do płaszczyzny podstawy tego ostrosłupa jest równy 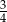3 4 . Oblicz pole powierzchni bocznej tego ostrosłupa.

Zadanie 6

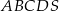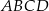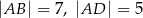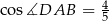Podstawą ostrosłupa ABCDS jest czworokąt wypukły ABCD , w którym |AB | = 7, |AD | = 5 oraz 4 c os∡DAB = 5 . Każda z krawędzi bocznych ostrosłupa ma długość 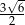√ - 3-6- 2 . Oblicz wysokość ostrosłupa.

Zadanie 7

Podstawą ostrosłupa 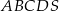ABCDS jest prostokąt 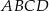ABCD , w którym 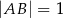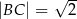|AB | = 1 , √ -- |BC | = 2 . Wszystkie krawędzie boczne tego ostrosłupa mają długość 1. Wyznacz cosinus kąta między dwiema sąsiednimi ścianami bocznymi tego ostrosłupa.

Zadanie 8

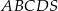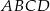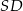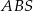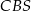Podstawą ostrosłupa ABCDS jest kwadrat ABCD . Krawędź boczna jest wysokością ostrosłupa, a jej długość jest dwa razy większa od długości krawędzi podstawy. Oblicz sinus kąta między ścianami bocznymi ABS i CBS tego ostrosłupa.

Zadanie 9

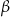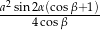Podstawą ostrosłupa jest trójkąt prostokątny o kącie ostrym i przeciwprostokątnej długości . Wszystkie ściany boczne ostrosłupa są nachylone do płaszczyzny podstawy pod kątem . Wykaż, że pole powierzchni całkowitej tego ostrosłupa jest równe a2sin2α(cosβ+1) 4 cosβ .

Wersja PDF