/Szkoła średnia/Zadania maturalne/Matura 2023/Polygon matematyczny

Planimetria – trójkąty poziom rozszerzony

Zadanie 1

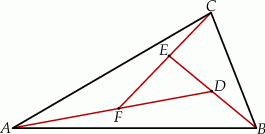
W trójkącie 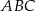ABC poprowadzono odcinki 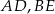AD ,BE i 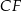w ten sposób, że punkty 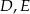D ,E i 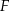są środkami odpowiednio odcinków 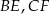BE ,CF i 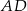. Wykaż, że pole trójkąta 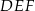DEF jest siedem razy mniejsze od pola trójkąta ABC .

Zadanie 2

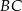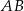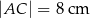Bok trójkąta ABC jest średnicą okręgu opisanego na tym trójkącie. Bok jest o 4 cm krótszy od boku oraz |AC | = 8 cm . Oblicz pole trójkąta 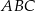ABC oraz długość promienia okręgu wpisanego w ten trójkąt.

Zadanie 3

Na okręgu o promieniu 1 opisano trójkąt prostokątny, którego przyprostokątne mają długości i .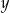

Wyznacz 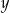jako funkcję i określ dziedzinę tej funkcji.
Sporządź wykres tej funkcji.

Zadanie 4

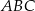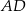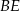W trójkącie ostrokątnym ABC wysokości i przecinają się w punkcie 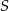. Wiadomo, że 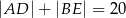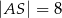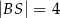|AD |+ |BE | = 20 , |AS | = 8 , |BS | = 4 . Wyznacz długości odcinków 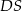i .

Zadanie 5

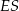W trójkąt równoramienny 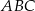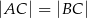ABC ( |AC | = |BC | ) o długości podstawy 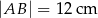|AB | = 12 cm wpisano kwadrat o boku długości 5 cm. Oblicz pole trójkąta ABC .

Zadanie 6

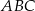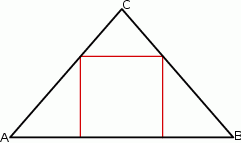
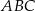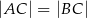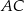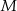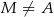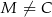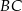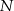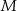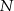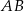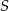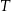Dany jest trójkąt równoramienny ABC , w którym |AC | = |BC | . Na ramieniu tego trójkąta wybrano punkt ( M ⁄= A i M ⁄= C ), a na ramieniu wybrano punkt . Przez punkty i poprowadzono proste prostopadłe do podstawy tego trójkąta, które wyznaczają na niej punkty i . Wykaż, że jeżeli 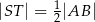|ST | = 1|AB | 2 , to |AM | = |CN | .

Zadanie 7

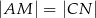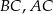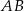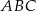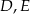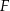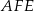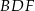Na bokach BC ,AC i trójkąta ABC wybrano odpowiednio punkty D ,E i . Wykaż, że jeżeli okręgi opisane na trójkątach AF E i BDF są styczne, to punkt 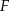leży na okręgu opisanym na trójkącie CED .

Zadanie 8

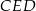Wyraź pole trójkąta w zależności od długości jednego z jego boków i miar kątów doń przyległych.

Zadanie 9

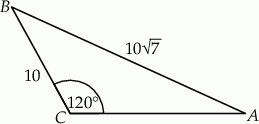
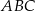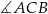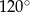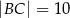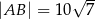Dany jest trójkąt rozwartokątny ABC , w którym ∡ACB ma miarę 120∘ . Ponadto wiadomo, że |BC | = 10 i -- |AB | = 10√ 7 (zobacz rysunek). Oblicz długość trzeciego boku trójkąta ABC .

Zadanie 10

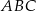Dany jest trójkąt prostokątny równoramienny 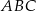ABC . Punkty 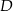i 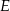dzielą przeciwprostokątną 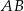na trzy odcinki równej długości. Oblicz cosinus kąta DCE .

Zadanie 11

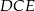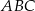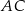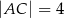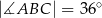W trójkącie równoramiennym ABC o podstawie dane są: |AC | = 4 oraz ∘ |∡ABC | = 36 . Odcinek 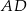jest odcinkiem dwusiecznej kąta 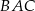BAC (zobacz rysunek).

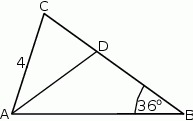
Oblicz długość odcinka .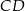

Zadanie 12

W trójkącie 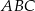ABC długości boków 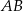i 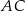są odpowiednio równe 4 i 6, a długość środkowej 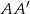′ AA jest równa 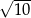√ --- 10 . Oblicz długość boku .

Zadanie 13

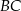Na bokach trójkąta zbudowano kwadraty o polach 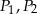P 1,P2 i 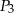(zobacz rysunek)

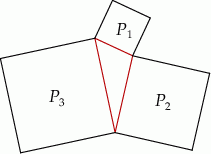
Wykaż, że 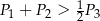P 1 + P 2 > 12P3 .

Zadanie 14

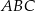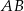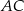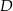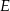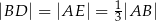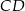Dany jest trójkąt równoboczny ABC . Na bokach i wybrano punkty – odpowiednio – i takie, że 1 |BD | = |AE | = 3|AB | . Odcinki i 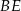przecinają się w punkcie 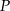(zobacz rysunek).

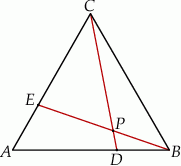
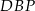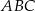Wykaż, że pole trójkąta DBP jest 21 razy mniejsze od pola trójkąta ABC .

Wersja PDF