/Szkoła średnia/Zadania maturalne/Matura 2023/Polygon matematyczny

Stereometria – objętość poziom rozszerzony

Zadanie 1

Odległość wierzchołka sześcianu od przekątnej sześcianu (do której dany wierzchołek nie należy) jest równa 4 cm. Oblicz objętość sześcianu.

Zadanie 2

Krawędź boczna ostrosłupa prawidłowego trójkątnego ma długość 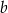i tworzy z płaszczyzną podstawy kąt o mierze . Jaką objętość ma ten ostrosłup?

Zadanie 3

Podstawą ostrosłupa 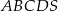ABCDS jest trapez prostokątny, w którym jedna z podstaw ma długość 7, a jedna z przekątnych ma długość 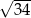√ --- 3 4 . Krawędź 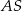jest wysokością ostrosłupa oraz 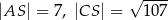√ ---- |AS | = 7 , |CS | = 107 . Oblicz objętość tego ostrosłupa.

Zadanie 4

Podstawą ostrosłupa jest równoramienny trójkąt prostokątny. Każda krawędź boczna ma długość 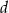i jest nachylona do płaszczyzny podstawy pod kątem . Oblicz objętość tego ostrosłupa.

Zadanie 5

Podstawą ostrosłupa ABCDS jest prostokąt ABCD o bokach długości i 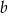. Krawędź 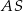jest prostopadła do płaszczyzny podstawy. Odległość wierzchołka 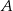od krawędzi 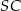jest równa 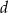. Wyznacz objętość tego ostrosłupa.

Zadanie 6

Podstawą ostrosłupa 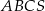ABCS jest trójkąt równoramienny 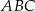ABC , w którym 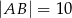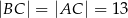|AB | = 10 , |BC | = |AC | = 1 3 i spodek wysokości ostrosłupa należy do jego podstawy. Każda wysokość ściany bocznej poprowadzona z wierzchołka 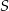ma długość 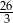26 -3 . Oblicz objętość tego ostrosłupa.

Zadanie 7

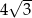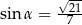W ostrosłupie prawidłowym trójkątnym wysokość ściany bocznej prostopadła do krawędzi podstawy ostrosłupa jest równa √ -- 4 3 i tworzy z krawędzią boczną kąt taki, że √ -- --21 sinα = 7 . Oblicz objętość tego ostrosłupa.

Zadanie 8

Podstawą ostrosłupa jest romb o boku długości 18 cm. Każda ze ścian bocznych tworzy z płaszczyzną podstawy kąt 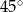∘ 45 . Pole powierzchni bocznej ostrosłupa jest równe 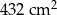2 432 cm . Oblicz jego objętość.

Zadanie 9

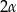W ostrosłup prawidłowy czworokątny wpisano kulę o promieniu . Ściana boczna ostrosłupa nachylona jest do płaszczyzny podstawy pod kątem . Oblicz objętość tego ostrosłupa.

Zadanie 10

Ostrosłup prawidłowy trójkątny przecięto płaszczyzną, która przechodzi przez krawędź podstawy długości oraz jest prostopadła do przeciwległej krawędzi bocznej. Płaszczyzna ta jest nachylona do płaszczyzny podstawy pod kątem . Oblicz objętość ostrosłupa.

Zadanie 11

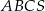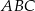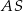W ostrosłupie ABCS podstawa ABC jest trójkątem równobocznym o boku długości . Krawędź jest prostopadła do płaszczyzny podstawy. Odległość wierzchołka 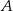od ściany 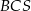BCS jest równa 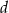. Wyznacz objętość tego ostrosłupa.

Wersja PDF