/Szkoła średnia/Zadania maturalne/Matura 2023/Polygon matematyczny

Optymalizacja – funkcje poziom rozszerzony

Zadanie 1

Wyznacz przedziały monotoniczności funkcji 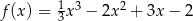1 3 2 f (x) = 3x − 2x + 3x− 2 .

Zadanie 2

Wyznacz najmniejszą 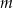i największą 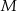wartość funkcji 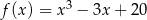f (x) = x3 − 3x + 20 w przedziale ⟨− 3;3⟩ .

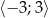Zadanie 3

Wyznacz wartość największą i najmniejszą funkcji 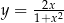y = -2x2 1+x w przedziale ⟨− 2;2 ⟩ .

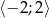Zadanie 4

Dana jest funkcja 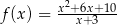f(x ) = x2+6x+10- x+ 3 .

Określ przedziały monotoniczności tej funkcji.
Znajdź ekstrema lokalne funkcji .

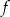Zadanie 5

Wyznacz wszystkie wartości parametru 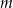, dla których funkcja 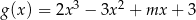g (x) = 2x3 − 3x2 + mx + 3 ma ekstremum lokalne równe 10.

Zadanie 6

Dla jakiej wartości parametru 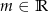m ∈ R funkcja 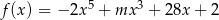f(x) = − 2x5 + mx 3 + 28x + 2 ma ekstremum w punkcie x = 2 ?

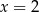Zadanie 7

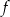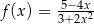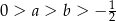Dana jest funkcja określona wzorem -5−4x f(x) = 3+ 2x2 dla każdej liczby rzeczywistej , oraz dwie liczby: 0 > a > b > − 1 2 . Oblicz wartość wyrażenia

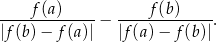
----f-(a)---- -----f(b)---- |f(b) − f(a)| − |f(a) − f(b )|.

Zadanie 8

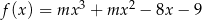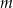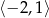Maksymalny przedział, na którym funkcja f (x) = mx 3 + mx 2 − 8x− 9 jest malejąca ma długość 2. Oblicz wartość parametru oraz wyznacz największą wartość funkcji na przedziale ⟨−2 ,1⟩ .

Wersja PDF