/Szkoła średnia/Zadania maturalne/Matura 2023/Polygon matematyczny

Stereometria – przekroje poziom rozszerzony

Zadanie 1

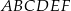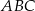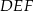Dany jest graniastosłup prawidłowy trójkątny ABCDEF o podstawach ABC i DEF i krawędziach bocznych 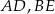AD ,BE i 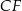(zobacz rysunek). Krawędzie boczne graniastosłupa mają długość 8, a tangens kąta między wysokością trójkąta 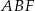ABF poprowadzoną z wierzchołka 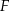i płaszczyzną podstawy 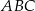ABC tego graniastosłupa jest równy 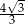4√3- 3 . Oblicz pole trójkąta ABF .

Zadanie 2

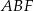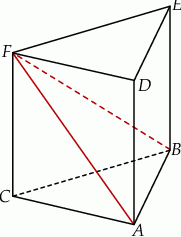
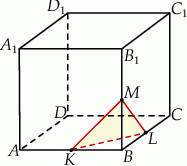
Przez środki trzech różnych krawędzi sześcianu 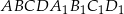ABCDA 1B 1C1D 1 wychodzących z wierzchołka 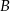poprowadzono płaszczyznę, która wyznaczyła przekrój bryły – trójkąt 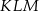KLM . Oblicz odległość wierzchołka 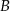od tego przekroju, jeżeli wiadomo, że długość krawędzi sześcianu wynosi 8.

Zadanie 3

Wysokość prawidłowego ostrosłupa sześciokątnego ma długość 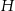, a krawędź podstawy ma długość . Wyznacz pole przekroju wyznaczonego przez krótszą przekątną podstawy i wierzchołek ostrosłupa.

Zadanie 4

Dany jest graniastosłup prawidłowy trójkątny o krawędzi podstawy i wysokości 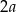. Graniastosłup przecięto płaszczyzną przechodzącą przez krawędź dolnej podstawy i środek ciężkości górnej podstawy. Oblicz pole otrzymanego przekroju.

Zadanie 5

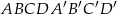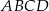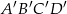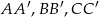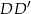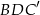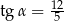Dany jest graniastosłup prawidłowy czworokątny ABCDA ′B′C′D ′ o podstawach ABCD i A ′B ′C′D ′ , oraz krawędziach bocznych AA ′,BB ′,CC ′ i DD ′ . Oblicz pole trójkąta BDC ′ wiedząc, że przekątna ściany bocznej ma długość 13 i jest nachylona do podstawy pod takim kątem , że 12 tg α = 5 .

Zadanie 6

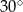Dany jest ostrosłup prawidłowy trójkątny, w którym długość krawędzi podstawy jest równa . Kąt między krawędzią boczną i krawędzią podstawy ma miarę 30 ∘ . Ostrosłup przecięto płaszczyzną przechodzącą przez krawędź podstawy i środek przeciwległej jej krawędzi bocznej. Sporządź rysunek ostrosłupa i zaznacz otrzymany przekrój. Oblicz pole tego przekroju.

Zadanie 7

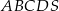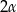Krawędź podstawy ostrosłupa prawidłowego czworokątnego ABCDS ma długość . Ściana boczna jest nachylona do płaszczyzny podstawy ostrosłupa pod kątem 2 α . Ostrosłup ten przecięto płaszczyzną, która przechodzi przez krawędź podstawy i dzieli na połowy kąt pomiędzy ścianą boczną i podstawą. Oblicz pole powstałego przekroju tego ostrosłupa.

Wersja PDF