Zadanie nr 1290584
Z pojemnika, w którym są dwa losy wygrywające i trzy losy puste, losujemy dwa razy po jednym losie bez zwracania. Oblicz prawdopodobieństwo, że otrzymamy co najmniej jeden los wygrywający. Wynik przedstaw w postaci ułamka nieskracalnego.
Rozwiązanie
Jeżeli za zdarzenia sprzyjające przyjmiemy pary otrzymanych losów to mamy
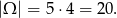
Sposób I
Zdarzenia sprzyjające są trzech typów:
Oba losy są wygrywające: są dwa takie zdarzenia (bo odróżniamy od siebie każde dwa losy).
Pierwszy los jest wygrywający, a drugi przegrywający: jest 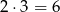 takich zdarzeń.
takich zdarzeń.
Drugi los jest wygrywający, a pierwszy przegrywający: jest 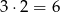 takich zdarzeń.
takich zdarzeń.
Zatem prawdopodobieństwo wynosi
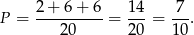
Sposób II
Tym razem z zdarzenia elementarne przyjmijmy nieuporządkowane pary wylosowanych losów, czyli
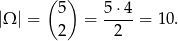
Policzmy prawdopodobieństwo zdarzenia przeciwnego 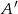 , czyli zdarzenia, w którym wylosowaliśmy dwa losy przegrywające. Zdarzeń sprzyjających
, czyli zdarzenia, w którym wylosowaliśmy dwa losy przegrywające. Zdarzeń sprzyjających 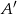 jest
jest
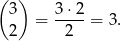
Zatem
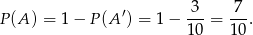
Odpowiedź: